Inscription / Connexion Nouveau Sujet
régimes transitoires d'un circuit RLC série
Bonsoir,
J'ai des questions concernant le cours sur les régimes transitoires d'un circuit RLC série.
On étudie le circuit sur l'image ci-dessous.
Initialement, le condensateur est déchargé. A t=0, on place l'interrupteur en position 1. On observe alors la réponse du circuit RLC série à un échelon de tension. Lorsque le régime permanent est atteint, le condensateur est chargé : u=E et l'intensité dans le circuit est nulle : i=0.
On bascule alors l'interrupteur en position 2. On observe le régime libre du circuit RLC série, correspondant à la décharge du condensateur.
Dans le II de mon cours, intitulé réponse à un échelon de tension, il y a écrit que la solution de l'équation différentielle s'écrit u=ulibre+uforcé. Pourquoi ? u est une variable additive dans le temps ?
Je ne trouve pas non plus cela cohérent (même si ça l'est forcément c'est juste que j'ai du mal à comprendre) qu'on nous dise en début de ce paragraphe : " A t=0 l'interrupteur est en position 1." puisque j'imagine que d'après le titre de ce paragraphe, on se situe après l'étude du régime libre donc on n'est plus à t=0. Et si jamais on "repart" de 0 alors pourquoi d'un côté on "annule" ce qui s'est passé avant en repartant de 0 et de l'autre on considère quand même ulibre dans le calcul de u ?
Merci d'avance pour vos explications !
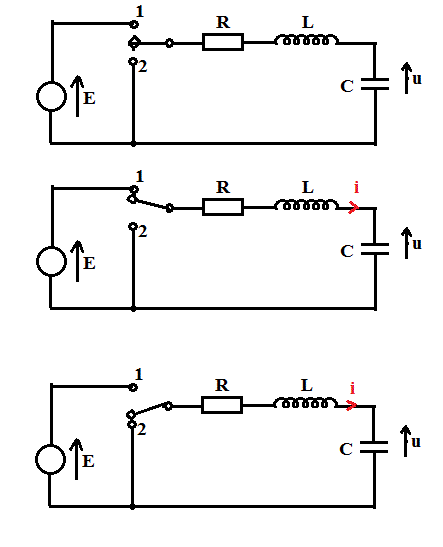
Dessin du milieu :
E = R.i + L.di/dt + u
avec i = C.du/dt
--> E = R.C.du/dt + LC.d²u/dt² + u
d²u/dt² + (R/L).du/dt + (1/(LC)).u = E/(LC)
C'est l'équation différentielle en u, il faut la résoudre (en tenant compte des conditions initiales) pour déterminer u(t)
Ensuite, cest purement mathématique, il a été démontré mathématiquement que les solutions de cette équation peuvent se trouver en ajoutant
a) Les solutions de d²u/dt² + (R/L).du/dt + (1/(LC)).u = 0
b) une solution particulière de l'équation complète, soit donc de d²u/dt² + (R/L).du/dt + (1/(LC)).u = E/(LC)
Une solution particulière est facile à trouver, par exemple u constante telle que (1/(LC)).u = E/(LC) (alors du/dt et d²u/dt² = 0)
--> u = E (1) est une solution particulière de d²u/dt² + (R/L).du/dt + (1/(LC)).u = E
Il faut donc encore trouver les solutions de d²u/dt² + (R/L).du/dt + (1/(LC)).u = 0
Pour ce faire, il faut trouver les solutions de p² + p.(R/L).du/dt + (1/(LC)) = 0
Pas de problème, car c'est une simple équation du decond degré, spot p1 et p2 ces 2 solutions (qui peuvent être réelles ou complexe)
Si elles sont complexes, on aura un système oscillatoire amorti, si elles sont réelles, u tendra vers sa valeur finale sans oscillations.
p² + p.(R/L).du/dt + (1/(LC)) = 0
p = [-(R/L) +/- ((R/L)² - 4/(LC))^(1/2]/2
p = [-(R/L) +/- (1/(LC))*(R²C²-4LC)^(1/2]/2
Si R²C²-4LC < 0; alors les p sont complexes et la réponse sera oscillatoire
Si R²C²-4LC > 0; alors les p sont réels et la réponse ne sera pas oscillatoire
Supposons (pas envie de traiter tous les cas) que R²C²-4LC < 0, on a alors :
p = [-(R/L) +/- (1/(LC))*i* RCarrée(4LC-R²C²)]/2
p = -R/(2L) +/- (1/(2LC))*i* RCarrée(4LC-R²C²)
p = alpha +/- i.Omega (avec alpha = -R/(2L) et w = RCarrée(1/(LC) - (R²/4L²))
Les solutions de d²u/dt² + (R/L).du/dt + (1/(LC)).u = 0, sont alors : u = e^(-alpha*t) * (A.cos(omega*t) + B.sin(omega*t)) (2)
Les solutions générales (toutes) de d²u/dt² + (R/L).du/dt + (1/(LC)).u = E sont la somme de (1) et de (2) -->
u(t) = E + e^(-alpha*t) * (A.cos(omega*t) + B.sin(omega*t)) (Avec A et B des constantes)
Les valeurs de A et B doivent être déterminées à partir des conditions initiales ... qui sont ici : u(0) = 0 et i(0) = 0
u(0) = 0 --> 0 = E + 1 * A --> A = -E
u(t) = E + e^(-alpha*t) * (-E.cos(omega*t) + B.sin(omega*t))
avec i = C.du/dt --> i = C * ( -alpha * e^(-alpha*t) * (-E.cos(omega*t) + B.sin(omega*t)) + e^(-alpha*t) * (E*omega.sin(ometa*t) + B.omega*cos(omega*t) )
i(0) = C * ( -alpha * (-E) + (B.omega)) = 0
B = -E * alpha/omega
et donc finalement :
u(t) = E + e^(-alpha*t) * (-E.cos(omega*t) -E * alpha/omega.sin(omega*t))
u(t) = E * [1 - e^(-alpha*t) * (cos(omega*t) + alpha/omega.sin(omega*t))]
Aux erreurs près, rien relu.
lim(t --> +oo) u(t) = E
-----------
Dessin du bas, on remet t = 0 à l'instant où l'interrutpeur passe en position 2
R.i + L.di/dt + u = 0
avec i = C.du/dt
--> R.C.du/dt + LC.d²u/dt² + u = 0
d²u/dt² + (R/L).du/dt + (1/(LC)).u = 0
On trouve évdemment le même type de solutions que dans le cas précédent ... mais en remplaçant E par 0.
u(t) = e^(-alpha*t) * (A.cos(omega*t) + B.sin(omega*t)) (Avec A et B des constantes)
Les valeurs de A et B doivent être déterminées à partir des conditions initiales ... qui sont ici : u(0) = E et i(0) = 0
u(0) = E = A
u(t) = e^(-alpha*t) * (E.cos(omega*t) + B.sin(omega*t))
i = C.du/dt
i = -alpha * e^(-alpha*t) * (E.cos(omega*t) + B.sin(omega*t)) + e^(-alpha*t) * (-E.omega.sin(omega*t) + B.omega.cos(omega*t))
i(0) = 0 -->
-alpha * E + B.omega = 0
B = E * alpha/omega
u(t) = E * e^(-alpha*t) * (cos(omega*t) + alpha/omega * sin(omega*t))
Aux erreurs près, rien relu.
Et lim(t--> +oo) u(t) = 0

Bonjour Kiecane
Je ne vais pas refaire l'étude du circuit RLC série en régime transitoire : tu as surement étudié cela en détail en cours et le message précédent rappelle l'essentiel. Je vais juste, sans être du tout certain de répondre à tes préoccupations, rebondir sur ta phrase :
Dans le II de mon cours, intitulé réponse à un échelon de tension, il y a écrit que la solution de l'équation différentielle s'écrit u=ulibre+uforcé. Pourquoi ? u est une variable additive dans le temps ?
Je pense, sans en être certain, que ton professeur note ulibre la solution de l'équation homogène :
Quel que soit le type de régime obtenu, l'expression de ulibre fait intervenir deux constantes A et B mais attention[:b] car l'erreur est fréquente chez les étudiants qui abordent pour la première fois cette étude : A et B ne doivent pas être déterminées pour l'instant. [b]Ce n'est pas cette solution "libre" qui doit satisfaire les conditions initiales, c'est la solution générale. Et justement : cette solution générale est la somme de ulibre et d'une solution particulière qui dépend du générateur placé aux bornes du dipôle RLC série. Ton professeur semble noter uforcé cette solution particulière qui, dans le cas d'un échelon de tension, vaut tout simplement E.
On obtient les constantes A et B en écrivant que u=ulibre+uforcé satisfait les conditions initiales. Tes interrogations sur les "t=0" ne sont plus fondées...
Remarque : l'expression uforcé est peu utilisée dans ce contexte. En général on l'utilise lorsque le générateur branché aux bornes du dipôle RLC série est un générateur de tension périodique de pulsation
 : la solution particulière est alors une solution de même pulsation que celle du générateur. Par exemple : si la fém du générateur est :
: la solution particulière est alors une solution de même pulsation que celle du générateur. Par exemple : si la fém du générateur est : Sous réserve bien sûr d'avoir correctement interprété ton message et les notations de ton professeur ...


