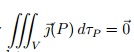
Bonjour,
Tu as commis une confusion je crois. Le vecteur densité de courant est à flux conservatif : le flux de ce vecteur est nul à travers toute surface fermée. C'est sur cette propriété que l'on se base pour affirmer, par exemple, que l'intensité d'un courant est la même à un instant donnée à travers toute section droite d'un circuit série.
Le théorème d'Ostrogradski  permet de montrer qu'un champ de vecteur est à flux conservatif seulement si sa divergence est nulle en tout point :
  avec () : surface fermée.
Or, l'équation de conservation de la charge électrique en régime variable quelconque conduit à la relation :

où désigne la densité volumique de charge en P.
En toute rigueur, le vecteur densité de courant n'est pas à flux conservatif en régime variable. Cependant, l'influence du terme   n'est sensible qu'en régime de très haute fréquence. On peut donc faire l'approximation du flux conservatif en régime lentement variable : c'est ce qu'on appelle l'approximation des régimes quasi permanents.