Inscription / Connexion Nouveau Sujet
Régime transitoire electronique
Bonjour, je suis en galère sur cet exercice :
j'ai déjà trouvé les equations différentielles, dans les deux cas, et je les ai résolu.
Pour la question 3, j'ai déterminé que R< racine(4L/C), puis que ksi vallait 0.162.
En revanche, pour la 4, je pense que T/2 >> 5 tau donc T > 10 tau, mais je ne vois pas comment faire l'application numérique
Merci d'avance
Je me suis dit que on basculait en régime permanant que le condensateur était chargé, donc qu'il s'était écoulé 5*tau.
Il fallait donc que la periode / 2 soit superieure à 5 fois cette constante de temps
Tout d'abord : d'accord avec tes résultats de la question 3.
Pour la question 4 : tu arrives bien à une condition de la forme :
T>10
où l'exponentielle est de la forme exp(-t/) mais n'est pas égal à R.C comme pour un circuit RC. Reprends l'expression de la solution uc=f(t) dans le cas du régime pseudo périodique. Éventuellement, ce document pourra t'aider. Tu y remarqueras que :
.
Ah oui j'aurais du voir que c'est l'augmentation de t qui diminue la valeur de l'exponentielle, donc l'amplitude des osillations. Et donc on a forcément lambda qui a la dimension d'un temps^-1 pour respecter l'exponentielle.
Donc on devrait trouver T > 3.8 mS et f > 263 HZ ?
J'ai lu trop vite ta réponse : revoir le sens de l'inégalité concernant la fréquence ! (étourderie j'imagine...)
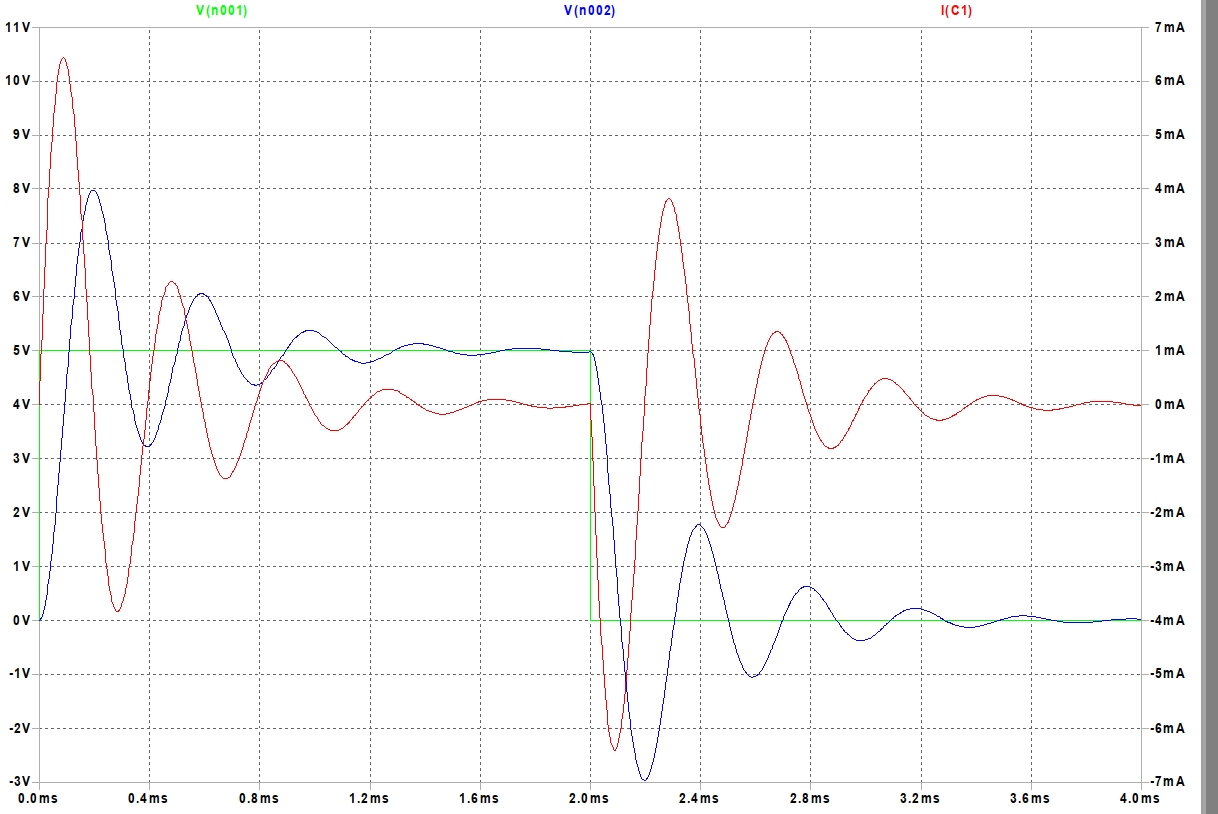
Si cela peut t'aider : voici une simulation avec :
en vert : la représentation des variations de la tension d'entrée avec une période de 4ms ;
en bleu : la représentation des variations de la tension uc(t) ;
en rouge : la représentation des variations de l'intensité i(t) ; tu peux vérifier que, à un facteur d'échelle près, cette courbe est la courbe dérivée de celle représentant les variations de uc(t).
A noter que uc(t) est fonction continue de t et que la présence de la bobine assure également la continuité de i(t)
Annuler
connectez vous