Niveau maths sup

régime transitoire du 2nd ordre

Posté par
ayudameplox 01-01-16 à 16:33

Bonjour,
je bloque à la première question de mon exercice :

montrer que $\frac{\mathrm{d^2i_{1}} }{\mathrm{d} t}+\frac{3}{RC}\frac{\mathrm{di_{1}} }{\mathrm{d} t}+\frac{1}{(RC)^2}i_{1}=0$

j'ai appliqué la loi des mailles loi/des nœuds mais je ne vois pas comment je pourrais me ramener à une telle expression, je dois sans doute manquer quelque chose
merci d'avance !

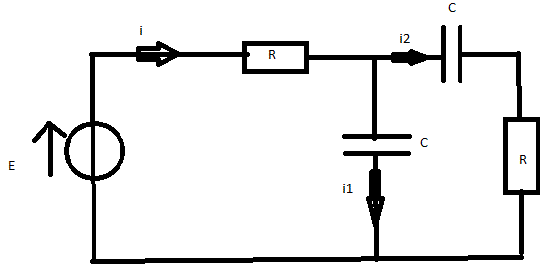
régime transitoire du 2nd ordre

Posté par re : régime transitoire du 2nd ordre 01-01-16 à 19:20

Bonsoir,
Tu as deux méthodes possibles :
la première consiste à étudier le circuit en régime sinusoïdal puis à remarquer que multiplier le complexe associé à une grandeur sinusoïdale par (jw)ⁿ est équivalent à prendre la dérivée n^ième de cette grandeur sinusoïdale . C'est la méthode la plus rapide dès que le circuit devient un peu compliqué.
La seconde, utilisable éventuellement ici, consiste à raisonner directement en valeur instantanées. Le chaînon manquant à ton raisonnement est peu-être celui-ci : (je note u la tension instantanée aux borne du condensateur de la branche parcourue par i1 :
$u=E-Ri=\frac{\int i_{1}\cdot dt}{C}=\frac{\int i_{2}\cdot dt}{C}+R\cdot i_{2}$
Tu te débarasses au dernier moment des primitives en dérivant par rapport à t l'expression obtenue.

Posté par re : régime transitoire du 2nd ordre 01-01-16 à 22:40

Bonsoir,
Voilà la seconde méthode qui s'appuie sur les trois égalités du message précédent. Je ne suis pas sûr qu'elle soit plus rapide que celle utilisant les complexes mais comme je ne suis pas certain que les impédances complexes aient été déjà étudiées dans ton cours...
Loi des nœuds :
$\begin{cases} \\ i_{2}=i-i_{1} & i_{2}=\frac{E}{R}-\frac{u}{R}-i_{1}=\frac{E}{R}-\frac{1}{RC}\int i_{1}dt-i_{1}\\ \\ \text{\text{dérivation par rapport au temps :}} & \frac{di_{2}}{dt}=-\frac{i_{1}}{RC}-\frac{di_{1}}{dt}\\ \\ \text{dérivation par rapport au temps de l'égalité message précédent} & i_{1}=i_{2}+RC\frac{di_{2}}{dt}\\ \\ \text{report dans cette égalité des expressions précédentes :}\\ \\ i_{1}=\frac{E}{R}-\frac{1}{RC}\int i_{1}dt-i_{1}+RC\left(-\frac{i_{1}}{RC}-\frac{di_{1}}{dt}\right) & 3i_{1}=\frac{E}{R}-\frac{1}{RC}\int i_{1}dt-RC\frac{di_{1}}{dt}\\ \\ \text{dérivation par rapport au temps :} & RC\frac{d^{2}i_{1}}{dt^{2}}+3\frac{di_{1}}{dt}+\frac{i_{1}}{RC}=0\\ \\ \text{En posant : \ensuremath{\omega_{0}=\frac{1}{RC}}} & \boxed{\frac{d^{2}i_{1}}{dt^{2}}+3\omega_{0}\cdot\frac{di_{1}}{dt}+\omega_{0}^{2}\cdot i_{1}=0} \\ \end{cases}$

Posté par re : régime transitoire du 2nd ordre 02-01-16 à 11:28

Bonjour,
Au cas où tu aurais déjà étudié l'utilisation des complexes en régime sinusoïdal, voici une méthode consistant à démontrer l'équation différentielle vérifiée par i1 en régime sinusoïdal puis à admettre que cette équation est valide en régime variable quelconque.
Le générateur est un générateur de tension sinusoïdale de f.ém. e. L'impédance de l'association série (R+C) vaut :

$\\ \underline{Z}=R+\frac{1}{jC\omega}=\frac{jC\omega+R}{jC\omega}$

Théorème de Millman :

$\boxed{\underline{u}=\frac{\frac{\underline{e}}{R}}{\frac{1}{R}+jC\omega+\frac{jC\omega}{1+jRC\omega}}=\frac{\underline{e}}{1+jRC\omega+\frac{jRC\omega}{1+jRC\omega}}=\frac{\underline{e}\left(1+jRC\omega\right)}{1+3jRC\omega+\left(jRC\omega\right)^{2}}}$

le complexe associé à l'intensité i1 est :

$\underline{i_{1}}=jC\omega\cdot\underline{u}=\frac{\underline{e}\cdot jC\omega\left(1+jRC\omega\right)}{1+3jRC\omega+\left(jRC\omega\right)^{2}}$
D'où :
$\underline{i_{1}}\left[1+3jRC\omega+\left(jRC\omega\right)^{2}\right]=\underline{e}\left(jC\omega+R\left(jC\omega\right)^{2}\right)$

Retour au domaine temporel comme expliqué précédemment :

$i_{1}+3RC\frac{di_{1}}{dt}+\left(RC\right)^{2}\frac{d^{2}i_{1}}{dt^{2}}=0\text{ car e = E : constante}$

$\text{En posant : \ensuremath{\omega_{0}=\frac{1}{RC}\text{ on obtient bien après division par \ensuremath{\left(RC\right)^{2}} : \ensuremath{\boxed{\frac{d^{2}i_{1}}{dt^{2}}+3\omega_{0}\cdot\frac{di_{1}}{dt}+\omega_{0}^{2}\cdot i_{1}=0}}}}}$

Posté par re : régime transitoire du 2nd ordre 02-01-16 à 13:18

Bonjour,
merci énormément de ton aide j'ai bien compris la seconde méthode grâce à toi
toutefois je n'ai pas bien compris la solution utilisant les impédances complexes (c'est un chapitre récent que je n'ai pas encore digéré )
je ne comprend pas que l'on puisse étudier ce circuit en régime sinusoïdal car ici on est face à une réponse à un échelon de tension ( constante donc non décomposable en sinusoïdes, non ?). Ou alors simplement que cela est possible uniquement durant le régime transitoire(=non constant) ? bref je suis un peu confus à ce niveau là...

Je fais aussi face à un petit problème (de maths je pense)
je ne comprend pas l'égalité suivante : $\\ R+\frac{1}{jC\omega}=\frac{jC\omega+R}{jC\omega}$

Dans la suite de l'exercice on s'intéresse aux valeurs de i1 à l'état initial et à l'état final
à l'état final elle est nulle si je ne me trompe pas, mais faire pour l'état initial ?
merci encore

Posté par re : régime transitoire du 2nd ordre 02-01-16 à 14:05

Merci pour ta clairvoyance ; j'ai commis une faute de frappe en recopiant ma formule sous latex : le numérateur est évidemment : 1+jRC. Heureusement : c'est seulement une faute de frappe car l'erreur n'est pas répercutée aux lignes suivantes.
As-tu compris la première méthode ? Si oui, laisse tomber provisoirement la seconde : tu pourras y revenir plus tard quand tu seras plus familiarisé avec les notations complexes.
Pour la suite, j'imagine que la date t = 0 correspond à la mise sous tension du circuit (fermeture d'un interrupteur sans rebond par exemple), les condensateurs étant déchargés. Tu dois savoir que la continuité de l'énergie fait qu'un condensateur impose la continuité de la tension à ces bornes : u(t=O-) = 0 = u-t=0+). A la date t = 0+, les condensateurs se comportent donc comme des fils de résistance négligeable. Refais un schéma du circuit dans ce cas particulier : tu montreras facilement : i₁(t=0+)=E/R

Posté par re : régime transitoire du 2nd ordre 02-01-16 à 15:42

J'ai oublié une précision dans le message précédent. Pour déterminer l'équation i₁=f(t), tu vas avoir besoin de i₁(t=0+) mais aussi de la dérivée de i₁ par rapport au temps à la même date et cela n'est pas tout à fait simple !
$\begin{cases} \\ E=Ri+u & E=R\left(i_{1}+i_{2}\right)+u\\ \\ \text{dérivation par rapport au temps :} & 0=R\frac{di_{1}}{dt}+R\frac{di_{2}}{dt}+\frac{du}{dt}\\ \\ \text{déjà démontré :} & \frac{du}{dt}=\frac{i_{1}}{C}\text{ et : \ensuremath{RC\frac{di_{2}}{dt}=i_{1}-i_{2}}}\\ \\ \text{cela conduit à :} & 0=R\frac{di_{1}}{dt}+\frac{i_{1}}{C}-\frac{i_{2}}{C}+\frac{i_{1}}{C}\\ \\ \text{cas particulier : t=0+ :} & i_{1}=\frac{E}{R}\quad;\quad i_{2}=0\\ \\ \text{cas particulier : t=0+ :} & \boxed{\left(\frac{di_{1}}{dt}\right)_{t=O^{+}}=\frac{-2}{RC}\left(i_{1}\right)_{t=0^{+}}=-\frac{2E}{R^{2}\cdot C}} \\ \end{cases}$
Remarque : j'ai eu besoin pour obtenir cete valeur, de résultats intermédiaires obtenue par la première méthode. Au final, elle se révèle sans doute plus rapide que celle utilisant les complexes, pour cet exercice bien sûr ; il ne faut pas trop généraliser.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

régime transitoire du 2nd ordre

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique