Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Régime transitoire d'une bobine

Posté par
Zonzon60 31-10-12 à 17:45

Bonjour,
J'ai commencé un exercice sur le régime transitoir et je bloque sur une question. L'erreur vient surement de mes réponses précédentes. Pourriez vous m'aider s'il vous plait?

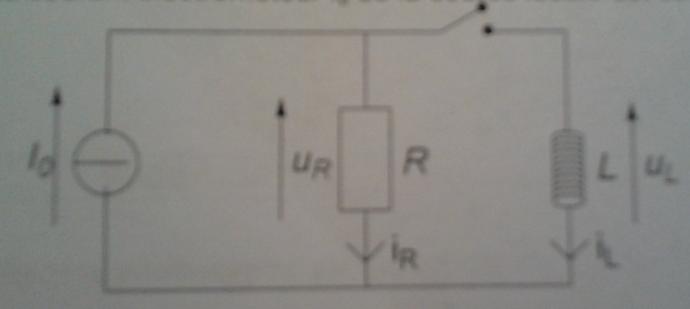
On envisage le circuit suivant dans lequel l'interrupteur K est ouvert depuis un long moment. A un instant choisi comme origine du temps, l'interrupteur est fermé. La bobine est assimilée à une inductance idéale. Le courant éléctromoteur Io de la source idéale est constant.

1) determiner sans calcul:
   a- les valeurs initiales des grandeurs uL, uR, iR, iL avant et juste après fermeture de l'interrupteur.
  
Avant fermeture de l'interrupteur:
uL= 0 V
uR= RiR
iR= I0 - iL
iL=  I0 - iR

après fermeture de l'interrupteur:
uL= L* (d( iL)/ dt)
uR= RiR
iR= I0 - iL
iL=  I0 - iR

    b- Les valeurs limites de ces grandeurs à l'issue du régime transitoire

uL= 0V
uR=  RIR
IR= I0 - IL
IL=  I0 - IR

2) Après fermeture de l'interrupteur:
   a- Etablir l'equation différentielle vérifiée par le courant iL

Ici j'ai trouvé que:
D'après la loi des mailles:
Io= L* (d( iL)/ dt) = RiR
donc l'équation différentielle serait: d( iL)/ dt = Io/L

La question suivante est de résoudre l'equation différentielle et d'exprimer les trois grandeurs uL, iR, iL.

Seulemement là je bloque! Je suppose que c'est parce que mon equation différentielle est fausse mais je ne vois pas comment trouver autre chose. Pourriez vous m'aider s'il vous plait?

Merci d'avance

Posté par
Marc35re : Régime transitoire d'une bobine 31-10-12 à 20:53

Bonsoir,

Citation :
On envisage le circuit suivant dans lequel...

Où est le circuit ?

Posté par
Zonzon60re : Régime transitoire d'une bobine 01-11-12 à 08:56

Navré, je pensais l'avoir mis.

Régime transitoire d\'une bobine

Posté par
Marc35re : Régime transitoire d'une bobine 01-11-12 à 10:15

Citation :
Avant fermeture de l'interrupteur:
uL = 0 V
uR = R iR
iR = I0 - iL
iL =  I0 - iR


UL = 0 ==> OK
uR = R iR ==> OK
iR = I0 - iL ==> non parce que iL = 0 donc iR = I0
iL =  I0 - iR ==> iL = 0
L'interrupteur est ouvert depuis longtemps donc pas de courant dans la bobine et p

Posté par
Marc35re : Régime transitoire d'une bobine 01-11-12 à 10:22

Envoi involontaire...
L'interrupteur est ouvert depuis longtemps donc pas de courant dans la bobine et pas de tension.

Et petite erreur :
uR = R iR ==> NON...UR = R I0

Posté par
Marc35re : Régime transitoire d'une bobine 01-11-12 à 10:36

Citation :
Juste après la fermeture de l'interrupteur:
uL = L (d( iL)/ dt)
uR = R iR
iR = I0 - iL
iL =  I0 - iR


UL = L (d( iL)/ dt) ==> en fait UL(0) = UR(0) = R I0
UR = R iR ==> UR = R I0
iR = I0 - iL ==> iL = 0 donc iR = I0
iL =  I0 - iR
==> iL = 0

Citation :
b- Les valeurs limites de ces grandeurs à l'issue du régime transitoire

UL= 0V
UR=  R iR
iR= I0 - iL
iL=  I0 - iR


UL = 0V ==> OK
UR =  R iR ==> UR = 0 parce que tout le courant passe par la bobine (résistance nulle)
iR = I0 - iL ==> iR = 0 (même raison)
iL=  I0 - iR ==> iL=  I0  (tout le courant passe par la bobine parce que résistance nulle)

Posté par
Marc35re : Régime transitoire d'une bobine 01-11-12 à 10:38

Citation :
D'après la loi des mailles:
I0 = L (d(iL)/ dt) = R iR

La loi des mailles ne dit pas ça...

Posté par
Marc35re : Régime transitoire d'une bobine 01-11-12 à 10:45

On peut dire :
U_L\,=\,U_R

\Large L\,\frac{di_L}{dt}\,=\,R\,i_R
Et on a (loi des noeuds) :
I_0\,=\,i_L\,+\,i_R\,\Rightarrow\,i_R\,=\,I_0\,-\,i_L
Donc :
\Large L\,\frac{di_L}{dt}\,=\,R\,\left(I_0\,-\,i_L\right)

\Large L\,\frac{di_L}{dt}\,+\,R\,i_L\,=\,R\,I_0
ou encore :
\Large \frac{di_L}{dt}\,+\,\frac{R}{L}\,i_L\,=\,\frac{R}{L}\,I_0

Posté par
Marc35re : Régime transitoire d'une bobine 01-11-12 à 10:52

En appliquant la loi des mailles au sens strict, il faudrait même écrire :
U_L\,-\,U_R\,=\,0\,\Rightarrow\,U_L\,=\,U_R\

Posté par
Zonzon60re : Régime transitoire d'une bobine 01-11-12 à 15:12

Tout d'abord merci pour vore aide. J'ai regardé tout ce que vous m'avez écrit en détail et j'ai compris mes erreurs. Il y a juste une petite chose que je ne suis pas sûre d'avoir comprise:
Pour les valeurs limites des grandeurs à l'issue du régime transitoire, R se comporte en fait, quand l'interrupteur est fermé, comme la résistance de la bobine? Et sachant que l'on a une bobine assimilée à une inductance idéale c'est pour cela qu'aucun courant et qu'aucune tension ne traverse la résistance? Est ce bien cela?

Posté par
Zonzon60re : Régime transitoire d'une bobine 01-11-12 à 16:21

En résolvant l'équation différentielle je trouve:

iL = I0*(1-exp((-R/L)t))
uL = RI0*exp((-R/L)t)
iR = I0*exp((-R/L)t)


La question suivante est portée sur l'étude énérgétique:
Exprimer l'énérgie reçue par chaque dipôle au cours du régime transitoire.

Pour cela j'ai utilisé la formule: L*(diL/dt) + RiL = RI0

J'ai multiplié l'ensemble par iL pour passer aux puissances.
Ensuite je suis passée aux énérgies par intégration.
Seulement je n'arrive pas à simplifier plus que cela:

(1/2)*R(I0)3 = 0infR(il)2dt + L0I0 (iL * (diL/dt)dt)

Posté par
Marc35re : Régime transitoire d'une bobine 01-11-12 à 18:59

Citation :
Pour les valeurs limites des grandeurs à l'issue du régime transitoire, R se comporte en fait, quand l'interrupteur est fermé, comme la résistance de la bobine?

Non, R est en parallèle sur la bobine. La résistance d'une bobine est en série avec la bobine.
Comme l'inductance est idéale, elle a une résistance nulle. Après le régime transitoire (==> régime permanent), on a une résistance nulle (la bobine) en parallèle sur une résistance R. Donc tout le courant passe par la résistance nulle (c'est-à-dire la bobine).
OK pour les solutions de l'équation différentielle. On voit que i_L\,\rightarrow\,I_0  et i_R\,\rightarrow\,0  quand t\,\rightarrow\,+\infty. C'est donc cohérent avec les résultats de la question précédente.
Pour l'étude énergétique pour chaque dipôle :
\large W_R\,=\,\int_0^{+\infty}\,R\,i_R^2\,dt\,=\,R\,I_0^2\,\int_0^{+\infty}\,\left(e^{-\frac{R}{L}t\right)^2\,dt\,=\,R\,I_0^2\,\int_0^{+\infty}\,e^{-\frac{2R}{L}t}\,dt\,=\,R\,I_0^2\,\left(-\frac{L}{2R}\right)\int_0^{+\infty}\,-\frac{2R}{L}\,e^{-\frac{2R}{L}t}\,dt\,=\,I_0^2\,\left(-\frac{L}{2}\right)\left[e^{-\frac{2R}{L}t}\right]_0^{+\infty}\,=\,\frac{1}{2}\,L\,I_0^2
Et pour la bobine, le principe est le même avec dW_L\,=\,\frac{1}{2}\,L\,i_L^2\,dt

Posté par
Zonzon60re : Régime transitoire d'une bobine 02-11-12 à 13:31

Je trouve exactement la même expression pour WL, est ce normal?
WL= (1/2)*LIo2

Posté par
Zonzon60re : Régime transitoire d'une bobine 02-11-12 à 14:06

La même expression que pour WR pardon

Posté par
Marc35re : Régime transitoire d'une bobine 02-11-12 à 16:27

Oui, ça me paraît normal parce que, si on calcule l'énergie fournie par le générateur, :
W_g\,=\,\int_0^{+\infty}I_0\,u\,dt\,=\,\int_0^{+\infty}I_0\,R\,I_0\,e^{-\frac{R}{L}t}\,dt\,=\,L\,I_0^2
Donc cela correspond bien à la somme des énergies de chaque dipôle.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !