Inscription / Connexion Nouveau Sujet
Régime transitoire
Bonjour
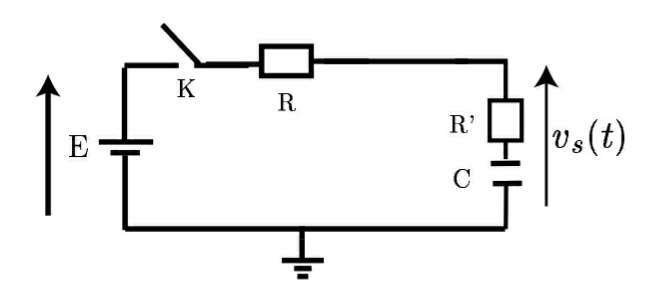
On suppose que le condensateur est initialement déchargé. A la fermeture de l'interrupteur K du circuit 1:
1- Établir l'équation différentielle que vérifie la tension Vc(t) aux bornes du condensateur .
2- en déduire l'évolution temporelle de Vs(t)
3- Calculer l'équation de la tangente à l'origine et tracer Vs(t). En déduire la constante du temps .
4- Exprimer la relation entre R et R' pour que la tension de sortie Vs soit à 75% de sa valeur maximale au temps t1= (R+R')C
J'ai établi l'équation différentielle
RtC( Vc)' + Vc = 0
Mais j'ai trouvé des difficultés à partir la deuxième question
J'aimerais bien aussi avoir des exos similaires de celle là et merci
Bonsoir
Tu as étudié en cours de mathématiques la résolution d'une équation différentielle du premier ordre. Cherche une solution faisant intervenir une exponentielle.
La question est bizarrement posée. À ce que je comprends, il faut commencer comme déjà dit par résoudre l'équation différentielle permettant d'obtenir Vc(t) puis d'obtenir Vs(t) en fonction de Ve(t), E et les résistances.
Au fait : tu es sûr de ton équation différentielle ? Il s'agit de la charge du condensateur lorsque l'interrupteur est fermé...
Non j'ai fait une erreur
On va trouver RtC(Vc)' + Vc = E
Après la résolution de cette équation on trouve Vc(t) = E ( 1-e^-t/RtC)
D'après la figue on peut déduire que
Vs(t) = Vc + VR'
Il faut ayssi3 trouver l'expression de i en fonction du temps ?
J'ai trouvé que i(t) = Ee^-t/RtC
Alors que Vs(t) =
Dans la 3ème question il est demandé de trouver l'équation de tangente , comment je vais faire?
On sait que l'équation de la tangente d'une fonction s'écrit sous forme : f(t) = f(to) + (t-to)f(to)'
J'ai appliqué cette relation à la fonction Vs(t) et j'ai trouvé Vs(t) = t + R'E
Cet résultat sera prévu ?
Ton expression de Vs(t) est nécessairement fausse car elle n'est pas homogène. En physique, pour qu'une somme (ou une différence) ait un sens, elle ne doit concerner que des grandeurs de même dimension physique. Or, ton expression fait intervenir la somme de l'inverse d'une résistance avec une exponentielle (grandeur de dimension un , grandeur sans dimension comme on dit encore).
On peut aussi déterminer Vs(t) à partir de la relation : Vs(t)=E-R.i(t) mais le calcul est à peine plus simple.
L'équation de la tangente que tu peux noter f(t) mais pas Vs(t) est fausse pour la même raison : il est impossible de soustraire (R'E) à un simple nombre réel : 1 !
Remarque plus générale : prendre l'habitude de contrôler systématiquement l'homogénéité des formules littérales obtenue permet d'éviter bien des erreurs et fautes d'étourderie....


