Inscription / Connexion Nouveau Sujet
Régime transitoire
Bonjour, j'ai un DM d'électricité et je ne m'en sors pas.
Je suis désolé mais je n'arrive pas à faire de schéma je vais donc essayer de décrire le montage du mieux possible.
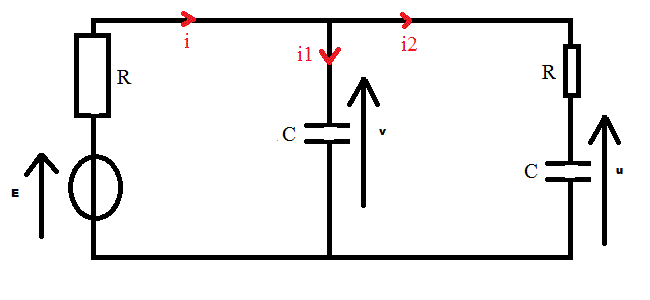
Sur la première branche, parcouru par un courant i dirigé vers le haut, on a un générateur de tension E dirigé vers, le haut et une résistance.
Sur la deuxième branche on un condensateur de tension v dirigé vers le haut.
Sur la troisième branche on a une résistance et un condensateur donc la tension u est dirigé vers le haut.
1) à t=0 on ferme un interrupteur et on me demande de trouver l'équa diff suivante :
d²u/dt² + (3/RC)du/dt + u(t)/(RC)² = E/(RC)²
2) Déterminer u(t)
3) Quel est le facteur de qualité Q du montage?
1) Je n'arrive pas à retrouver cette équa diff, j'ai fait 2 lois des mailles mais je ne vois pas comment on peut se retrouver avec une dérivée seconde.
2) J'ai trouver que u(t)=E.. Le delta de l'équation homogène associé est positif donc je cherche les solutions de la forme u(t)=Ae^r1t + Be^r2t .En utilisant les conditions initiales j'ai trouver que A=-B. Je trouve donc que les sol de l'équation homogène sont u(t) = 0. Et j'ajoute une solution particulière à savoir u(t) = E.
3)J'ai une formule dans mon cours : Q=Lw0/R Mais je ne vois pas ce qu'il faut faire.
Si vous pouviez m'aider ça serait super sympa. (je suis désolé si l'exercice n'est pas clair, j'ai fait de mon mieux)
salut à toi
voilà le circuit, je me trompe ? (j'ai oublié de dire : i dans la branche du générateur, i1 dans la première branche et i2 dans la 2e)
dans ce cas, il y a juste à écrire tout ce qu'on peut écrire !
i2 = C.dv/dt
i3 = C.du/dt
loi des noeuds :
i = i1+i2
loi des mailles :
v = R.i3 + u
E = R.i + v
plus qu'à mélanger ! tu peux y arriver ?
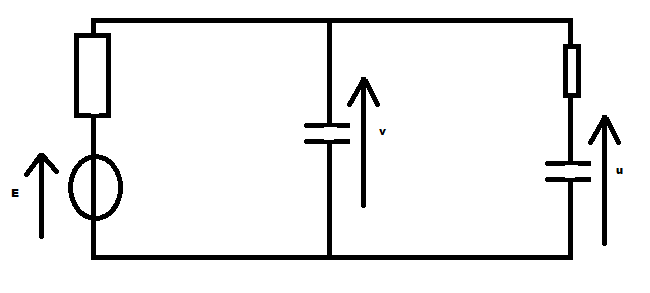
Attention, quelques bisbrouilles dans les notations dans le message de efte.
[img1]
i1 = C.dv/dt
i2 = C.du/dt
loi des noeuds :
i = i1+i2
loi des mailles :
v = R.i2 + u
E = R.i + v
-----
i = C.dv/dt + C.du/dt
v = RC.du/dt + u
E = R.i + v
-----
v = RC.du/dt + u
E = RC.dv/dt + RC.du/dt + v
-----
E = RC.d[RC.du/dt + u]/dt + RC.du/dt + RC.du/dt + u
E = R²C².d²u/dt² + RC.du/dt + RC.du/dt + RC.du/dt + u
E = R²C².d²u/dt² + 3RC.du/dt + u
d²u/dt² + (3/(RC)).du/dt + u/(RC)² = E/(RC)²
-----
Sauf distraction.
Merci beaucoup à tous les deux, c'était très clair, j'ai réussi à le faire !
Je ne veux pas abuser de votre gentillesse mais est-ce que vous trouver u(t)=E ?
Et pour la dernière question, je ne comprends pas ce que je dois faire, je dois juste marquer la formule ? (je n'ai aucune valeur numérique). De plus, dans la formule il y a de l'inductance, or il n'y a pas de bobine donc qu'est-ce que je dois faire ? Poser L=0 ?
2) alala oui mais u(t) = 0 c'est toujours une solution de l'équation homogène c'est sur ^^ mais ce n'est pas une solution très intéressante.
les deux racines de l'équa caractéristique sont [-3 +-  5 ]/(2RC) : ( à vérifier)
5 ]/(2RC) : ( à vérifier)
u(t) = E est bien une solution particulière.
On a donc : u(t) = E + A.e((-3+ 5)/(2RC)t) + B.e((-3-
5)/(2RC)t) + B.e((-3- 5)/(2RC)t)
5)/(2RC)t)
je ne sais pas où se trouvait ton interrupteur dans le circuit, surement dans la branche du générateur ? Ca nous donnerait u(0)=0 et i2(0)=0 donc du/dt(t=0) = 0
ça te donne A+B+E = 0 et (-3+ 5)A + (-3-
5)A + (-3- 5)B=0
5)B=0
donc tu peux avoir accès à A et B.
pour la question 3), il faut identifier avec la forme canonique d'une équa diff du second ordre : d²y/dt² + wo/(2Q). dy/dt + wo².y
si tu compares à ton équa diff, tu as : wo = 1/(RC) et Q= 1/6 (ce qui est compatible avec le régime apériodique qu'on avait trouvé)