Inscription / Connexion Nouveau Sujet
Régime sinusoïdal : lois de Kirchhoff
Bonjour j'ai un problème avec un exercice, une petite aide ne serait pas de refus ^^
Un lien vers le dessin du circuit que j'ai fait comme j'ai pu avec paint :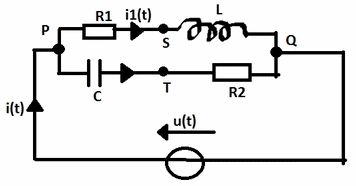 
Enoncé :
Pour le circuit représenté sur la figure, on donne :
U=250V ; f=50Hz ; R1= 100
; R2= 150 ; L
=75 et 1/C=200
Etablir les expressions littérales et calculer les valeurs numériques (en coordonnées polaires et cartésiennes) :
a) des impédances complexes Z1 et Z2 de chaque branche.
b) des intensités complexes I1 et I2.
c) de l'intensité totale I.
d) de la d.d.p UST. Le résultat obtenu était-il prévisible ?
Alors pour l'instant j'ai trouvé :
a) Z1= ZR + ZL= R1+Lj= 100+75j = 125*exp(36.87°) (je sais pas si l'angles est en degré ou en radian)
Z2= ZC + ZR2= 1/jC + R2 = 150-200j = 250*exp(25.82°)
b)I1= Im1*exp(jt) = Im*exp(j
i)*exp(jt)
I2=Im2*exp(ji)*exp(jt)
Après je ne vois pas comment trouver les valeurs numériques de ces deux intensités, je voulais essayer d'utiliser la formule U = Z1*I1 et ensuite calculer le module de I1 mais je ne sais pas si la donnée de l'énoncé U=250V est l'amplitude ou pas.
c) I=I1+I2 je n'ai pas les valeurs de I1 et I2 vu que j'ai pas calculé à la b)
d) Je ne vois pas comment faire non plus.
Merci d'avance à ceux qui m'aideront.
Edit Coll : image placée sur le serveur de l' 
Merci d'en faire autant la prochaine fois ! 
Dsl pour le double post mais j'ai oublié sur mon dessin i2(t) qui correspond à la flèche en dessous de celle de i1(t).
Salut,
a) je pense qu'il faut rester en radian de plus il maque le j dans exp
b) I1=U/Z1 = 250 exp(j100
t)/(100+75j)
= 250 exp(j100t)/(125*exp(a*j))
= 2 exp(j100t - a*j))
= 2 exp(j(100t - a))
avec a la valeur exacte dans l'expression Arc Cos (100/
(100²+75²))=a
Merci pour l'aide mais il y a un petit truc que je comprends pas, c'est comment on sait que le U donné dans l'énoncé est l'amplitude complexe ?
Ah oui d'accord et donc c'est forcément l'amplitude complexe. Parce que je confond les 2 amplitudes parce que souvent dans les exercices on retrouve Umsin(t+u) = Um*exp(jt) = Um*exp(jt)*exp(ju)
Et là je vois pas la différence entre Um et Um???
Annuler
connectez vous