Inscription / Connexion Nouveau Sujet
Régime sinusoïdal forcé
Bonjour je n'arrive pas à trouver comment résoudre la dernière question de cet exercice :
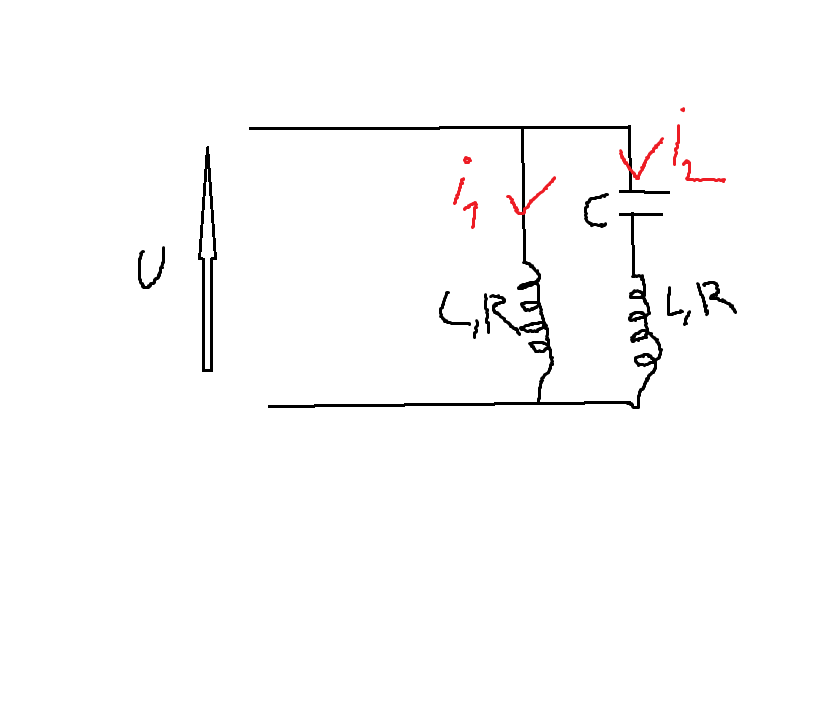
On considère le circuit ci-contre. On pose u = Um cos wt.
1) Déterminer les intensités efficaces des courants i1 et i2 et leurs déphasages  1 et
1 et  2.
2.
2) Pour quelle valeur de C, i1 et i2 sont-elles en quadrature ? On donne tan(a-b) = (tana - tanb)/(1+tana*tanb)
3) On veut que i1 et i2 soient non seulement en quadrature, mais en plus égales en valeurs efficaces.
Montrer que pour qu'il en soit ainsi, R, L et w doivent vérifier une certaine relation.
Pour la question 1) j'ai : valeurs efficaces de i1= Im1/rac(2) = Um/rac[ 2*( R^2 + (L*w)^2 ) ] avec Im1=Um/rac[ ( R^2 + (L*w)^2 ) ]
valeurs efficaces de i2= Im2/rac(2) = Um/rac[ 2*( R^2+(L*w - [1/(C*w)] )^2 ) ] avec Im2=Um/rac[ (R^2 + ( L*w - [1/(C*w)] )^2 ) ]
 1 = arctan(L*w/R) et
1 = arctan(L*w/R) et  2 = arctan( (LC*w^2 - 1)/RCw )
2 = arctan( (LC*w^2 - 1)/RCw )
Pour la question 2) j'ai :  1 -
1 -  2 =
2 =  pi/2
pi/2  C= L/(R^2+(Lw)^2)
C= L/(R^2+(Lw)^2)
Comme dit plus haut je n'arrive pas à faire la question 3, pouvez vous m'aider ?
Bonjour
D'accord avec tes expressions des intensités efficaces.
Pour les phases initiales : attentions aux signes.
Pour la question 3 : ils faut aussi tenir compte des intensités efficaces égales...
Petit oubli de ma part : les calculs sont plus simples sans mise au même dénominateur. Par exemple, tu as tout intérêt à laisser l'impédance du dipôle n° 2 sous la forme :
Bonjour
D'accord avec tes expressions des intensités efficaces.
Pour les phases initiales : attentions aux signes.
Pour la question 3 : ils faut aussi tenir compte des intensités efficaces égales...
Merci j'ai réussi a trouver je sais pas pourquoi je bloquais sur un truc aussi simple

Je ne comprends pas pourquoi le signe des phases à l'origine n'est pas bon par contre ?
Bonjour
D'accord avec tes expressions des intensités efficaces.
Pour les phases initiales : attentions aux signes.
Pour la question 3 : ils faut aussi tenir compte des intensités efficaces égales...
Merci j'ai réussi a trouver je sais pas pourquoi je bloquais sur un truc aussi simple

Je ne comprends pas pourquoi le signe des phases à l'origine n'est pas bon par contre ?
*Le signe des phases initiales pardon
Dans cet exercice, la phase initiale de u(t) est choisie nulle. Telle que la question est posée :
Cela dit : cela ne change rien à la suite. A titre de vérification, tu pourrais indiquer la relation simple que tu obtiens entre R,L et  à la question 3 ?
à la question 3 ?
Bonjour
D'accord avec tes expressions des intensités efficaces.
Pour les phases initiales : attentions aux signes.
Pour la question 3 : ils faut aussi tenir compte des intensités efficaces égales...
Merci j'ai réussi a trouver je sais pas pourquoi je bloquais sur un truc aussi simple

Je ne comprends pas pourquoi le signe des phases à l'origine n'est pas bon par contre ?
*Le signe des phases initiales pardon
Autant pour moi j'ai compris merci de votre aidevanoise
Dans cet exercice, la phase initiale de u(t) est choisie nulle. Telle que la question est posée :
Cela dit : cela ne change rien à la suite. A titre de vérification, tu pourrais indiquer la relation simple que tu obtiens entre R,L et
 à la question 3 ?
à la question 3 ?J'ai R^2(1/Lw) + L(1-2Lw) = 0
J'ai R^2(1/Lw) + L(1-2Lw) = 0
Plutot R^2 * (1/Lw) + L(1-2Lw) = 0 pour etre plus clair
J'ai R^2(1/Lw) + L(1-2Lw) = 0
Plutot R^2 * (1/Lw) + L(1-2Lw) = 0 pour etre plus clair
R^2 *( (1/Lw) - 2) + L(1-2Lw) = 0
J'ai bien fait de demander... Ton résultat est nécessairement faux car il n'est pas homogène. En physique on ne peut additionner ou soustraire que des grandeurs de même dimension.
Écrire (1-2L ) est faux : on ne peut soustraire à un simple nombre une grandeur ayant la dimension d'une impédance.
) est faux : on ne peut soustraire à un simple nombre une grandeur ayant la dimension d'une impédance.
Écrire ( (1/L ) - 2) est faux également pour la même raison.
) - 2) est faux également pour la même raison.
=0 que tu as oublié.
Cela peut se simplifier dans la mesure où toutes les grandeurs sont strictement positives.


