Inscription / Connexion Nouveau Sujet
Régime permanent. Incompréhension
Bonjour, alors j'ai un exercice à faire, et j'éprouve quelques difficultés à le terminer, si quelqu'un pourrait m'aider
Il s'agit d'un circuit composé d'un générateur et d'une capacité et d'une résistance. La résistance et la capacité étant en série.
Voici les différentes questions :
1) Exprimer les impédances complexes : d'un condensateur (C) , d'une bobine idéale (L) et d'une bobine (L,R)
Mes réponses sont les suivantes :
Zc= 1/(jcw) = -j/Cw ; Z(L)= jLw ; Z(L,R) = R+jLw
2) Exprimer l'impédance complexe d'une association série RC. Donner l'expression de son module et de son argument.
Z= R - j/Cw
Module de Z =  (R²+(-1/Cw)²)
(R²+(-1/Cw)²)
tan = -1/RCw
= -1/RCw
3) Exprimer l'amplitude de la tension mesurée aux bornes de ce dipôle en fonction de R,C, f et Io l'amplitude de l'intensité qui les traversent.
Alors là je n'ai aucune idée de comment faire. Si quelqu'un pourrait m'éclairer.
4) Exprimer le déphasage observé entre la tension aux bornes du dipôle et l'intensité qui le traverse.
ça non plus je ne sais pas comment procédé.
Peut être utilisé le fait que U=ZI par conséquent I=U/Z avec Z=R-j/Cw ?
5) Etablir l'équation différentielle (réelle) à partir de l'additivité des tensions réelles.
Je ne comprends pas non plus comment on pourrait l'établir
Pour terminer, il faut renouveler les question 2à5 pour un dipôle série RL
Donc pour la question 2)
Z= R+jLw module de Z=  (R²+(Lw)²
(R²+(Lw)²
Son argument : tan = Lw/R
= Lw/R
Merci aux personnes qui prendront le temps de me répondre ! 
Bonjour,
Tout d'abord, je suis étonné que tu n'as pas vu çà en cours.
Il faut se rappeler que tous les théorèmes vus en courant continu sont appliquables en alternatif sous réserve d'utiliser les valeurs complexes.
Pour un circuit R,L,C série, on a, en valeurs complexes
2)
|Z| = V[R² + (1/(wC))²] = (1/(wC)) * V(1 + w²R²C²) (avec V pour racine carrée)
Phi = -arctan(1/(wRC))
-----
3)
U = Z.I
|U| = |Z|.|I|
|U| = Io * (1/(wC)) * V(1 + w²R²C²)
---
4)
U = Z.I
U/I = Z
arg(U/I) = arg(Z)
arg(U) - arg(I) = arg(Z)
arg(U) - arg(I) = -arctan(1/(wRC))
La tension aux bornes du dipôle est en retard de arctan(1/(wRC)) sur l'intensité de courant qui le traverse.
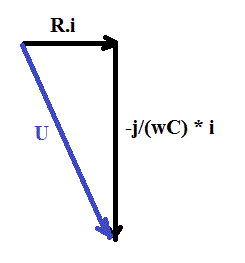
---
5)
u = r.i + L.di/dt
---
Sauf distraction. 
Merci à toutes les personnes qui ont pris le temps de répondre! J'ai absolument tout compris!
Bonne soirée 


