Inscription / Connexion Nouveau Sujet
régime libre circuit rlc série
Bonjour,
Le prof nous a donné des feuilles de cours que l'on doit complèter pendant les vacances mais je n'y arrive pas.
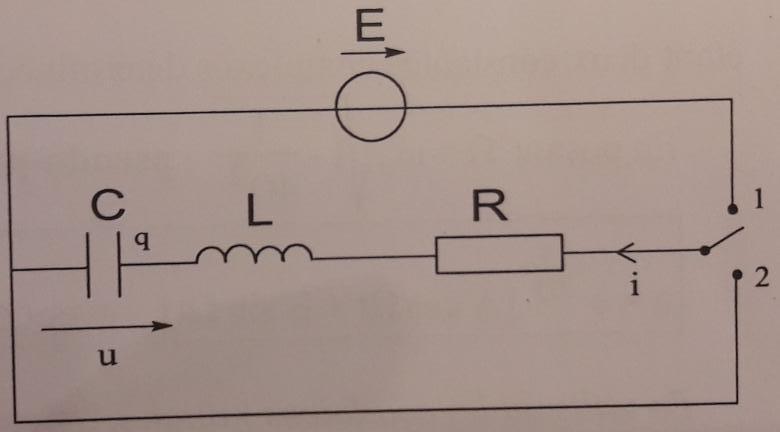
Sur la première, il nous donne le circuit suivant (cf ci-joint).
Enoncé :
Initialement, le condensateur est déchargé. A t=0, on place l'interrupteur en position 1. On observe alors la réponse du circuit RLC série à un échelon de tension. Lorsque le régime permanent est atteint, le condensateur est chargé : u=E et l'intensité dans le circuit est nulle : i=0.
On bascule alors l'interrupteur en position 2. On observe le régime libre du circuit RLC série, correspondant à la décharge du condensateur.
Etude du régime libre :
A t=0, l'interrupteur est basculé en position 2. Les conditions initiales sont : i(0+)=0 par continuité de l'intensité traversant la bobine et u(0+)=E par continuité de le tension aux bornes d'un condensateur.
Etablir l'équation différentielle en u :
J'ai fait une loi des mailles :
Je dérive et j'obtiens : mais je ne vois pas comment transformer les i en u....
Merci d'avance pour votre aide !
Hello
Je te dirais bien: c'est pas trop grave ... nous ne sommes qu'au début des vacances 
Plus sérieusement:
1) tu établis la relation qui lie u, q et C
2) tu te souviens que i = dq/dt
3) tu déroules ...
Et tu partages ici tes accomplissements et tes questionnements
Ensuite je dois trouver A' et B' dans la solution : sachant qu'on nous donne les conditions initiales :
et
J'ai réussi à trouver que A'=E mais je ne vois pas comment déterminer B' puisque dans tous les cas sin(0)=0
Comment je peux faire ?
(0) = 0 , mais on a aussi : i = C.du/dt
--> en t = 0 : i(0) = C.(du/dt)(0)
Et donc (du/dt)(0) = 0
...

Bonsoir,
J'ai trouvé A'=E et B'=
Dans la suite on considère toujours les mêmes conditions initiales mais on étudie le régime critique. On a
J'ai trouvé et B=E.
Enfin on étudie le régime apériodique où
et je trouve et
Dans un second temps, à t=0, l'interrupteur est en position 1. Les conditions initiales sont i(0+) =0 et u(0+)=0. On obtient l'équation différentielle :
La solution de cette équation est avec
solution générale de l'équation homogène et
la solution particulière telle que
.
Je devais trouver l'expression complète de la solution correspondant au régime pseudo-périodique.
J'ai trouvé : u=
Est-ce que tous ces résultats sont justes s'il-te-plaît ? 
Personnellement, cela me dérange d'avoir du wo, du Q et du dans la solution sans qu'il ne soit précisé nulle part ce que valent wo et Q et
Quand cela sera bien défini et à supposer que ce soit correct, il y a des problèmes de signe dans ta réponse finale.
Au premier coup d'oeil; on voit par exemple que en t = 0, ta réponse donne u(0) = -E

Bonsoir,
On a :
wo=
Q=
C'est moi qui ait déterminé wo et Q donc il y a potentiellement une erreur et par contre  nous ait donné.
nous ait donné.
Pour mon dernier paragraphe, j'ai déterminé (c'est un nouveau) mais c'est peut-être faux aussi.



