Bonjour, j'ai un exercice que je n'arrive pas à faire.

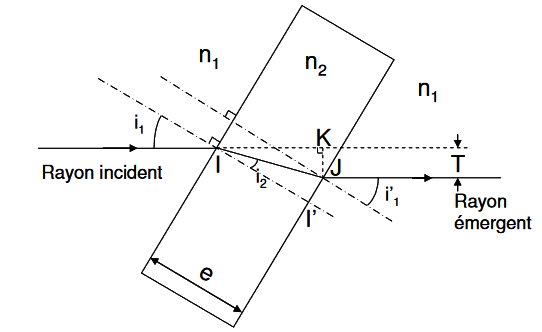
Un pinceau de rayons parallèles arrive en incidence sur la lame parallèle suivante (image joint)

1.Justifier le parallélisme entre le rayon incident et le rayon émergent.
2. Exprimer la translation T que les rayons subissent lors de la traversée de la lame en fonction de i1, i2 et e.
3. Le chemin optique est augmenté par la traversée de la lame d'une quantité ∆. Exprimer cette quantité ∆ en fonction de i1, i2, n1, n2 et e

1. n1sin(i1) = n2sin(i2)
Au niveau du point J on a : n2sin(i2')=n1sin(i1'). i2' est l'angle créé par IJ et la droite sécante à J.

Ensuite j'ai un doute si je peux dire que les droites en pointillées sont parallèles. Mais si oui du coup i2=i2'.
sini2=sini2'. n2sini2=n2sini2'. n1sini1 = n1sini1'. i1 = i1'
Mais après je suis bloqué...