Inscription / Connexion Nouveau Sujet
réflexion miroir
Bonjour,
on a étudié une diffraction d'un faisceau sur un miroir incliné et on trouve une intensité
On a analysé cette fonction pour trouver les directions, donc les alpha ayant le maximum d'intensité .
On maintenant besoin de donner la relation entre et
pour avoir le maximum de diffraction.
J'ai un doute sur la signification de ce maximum de diffraction .
Est ce l'angle pour lequel on a le maximum d'intensité ?
Je pensais plutôt que c'étais l'angle maximal au dela duquel l'intensité est nulle ?
Merci d'avance pour vos éclaircissement 
Bonne soirée
Bonsoir
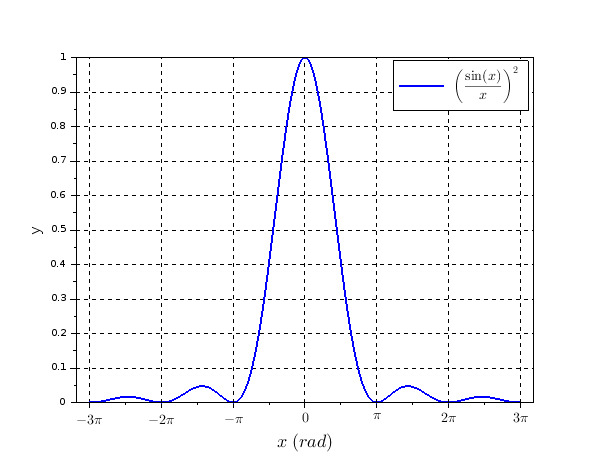
Tu as sûrement étudié en cours de math les variations de :
On obtient un maximum principal y=1 pour x=0. Je te laisse continuer...
Pour rappel : la courbe ci-dessous.
Bonsoir,
j'ai bien trouvé le maximum d'intensité pour
or les angles étant entre -pi/2 et pi/2 (réflexion par rapport à la normale) on peut écrire
Cet angle correspond à la direction du maximum d'intensité .
Correspond t il aussi au maximum de diffraction ?
Merci pour votre aide 
L'expression "maximum de diffraction" est un raccourci de langage (ou d'écriture !). Plus rigoureusement, il faut parler de "maximum de l'intensité diffractée" donc, avec tes notations, d'un maximum de I( ).
).


