Inscription / Connexion Nouveau Sujet
RDM charge lineique
Bonjour , je vous donne ici l énoncé de mon problème puis les solutions que j ai trouvés .
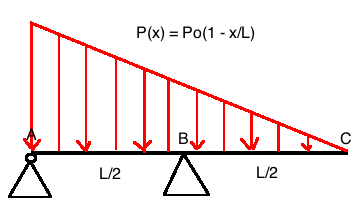
Soit une poutre de longueur L avec un appui double A et un appui simple au point B , le point B se situant au milieu de la poutre ( c est à dire à L/2) . Cette poutre est soumise a une charge repartie p(x) variable , verticale descendante entre les points À et C.
On donne p(x) = po (1-x/L)
Il est demandé d écrire au point A le torseur d action mecanique de la charge répartie sur la poutre . Méthode avec intégrale .
Mes resultat :
Résultant = po(L-x) (vecteur )y
Moment = po( (L^2)/2 - (xL)/2) ( vecteur )z
Pouvez vous m indiquer si ces resultat obtenu sont juste .
Merci de votre aide .
Salut !
Pourrais-tu :
1. Me faire un schéma de la situation (sur paint par exemple) ?
2. Me dire comment tu as trouvé tes réactions aux appuis ?

J'ai le même exercice a faire.
1) Ecrire au point A le torseur d'action mécanique de la charge répartie sur la poutre. vous utiliserez la méthode avec intégrales.
2)Ecrire les torseurs d'action mécanique des liaisons sur la poutre.
3) Déterminer l'expression des inconnues de liaison a partir du PFS appliqué à la poutre et écrit au point A.
4)En effectuant un calcul à droite de la coupe fictive, déterminer l'expression du torseur de cohésion en tout point du tronçon [BC]. Vous utiliserez la méthode avec intégrales.
5)Même question que la 4 mais avec un calcul à gauche de la coupe fictive sur le tronçon [AB].
6) Tracer les différents diagrammes.
Je vous met dans un autre message les résultats que j'ai trouvé.
Mes résulats :
1) {T(F/P)} au point A = Résultante => -(L/2)Po y
Moment => -(L^2/6)Po z
2) {T(Ar/P)}au point A = Résultante => Xax+Yay
Moment => 0
{T(As/P)}au point B = Résultante => Yby
Moment => 0
au point A = Moment =>(L/2)Ybz
3) PFS
{T(Ar/P)} + {T(As/P)} + {T(F/P)} = 0
Résultantes
Xax + Yay + Yby - (L/2)Poy
Donc Ya + Yb = (L/2) Po
Moments
-(L^2/6)Poz + Yb(L/2)Poy = 0
Donc Yb = (L/3) Po
et Ya = (L/6) Po
4) {Tcoh}au point G = Résultante => -(L^3/6)Poy
Moment => -(L^4 /12)Poz
je suis resté bloqué ici car je ne suis pas sur de mes résultats.
Si quelqu'un pouvais m'aider, merci