Inscription / Connexion Nouveau Sujet
RDM - Charge à ELU
Bonjour,
Je suis actuellement entrain de faire cet exercice, depuis 2 jours. Malheureusement je coince. Je remercie les personnes qui apporteront leur aide.
Énoncé de l'exercice:
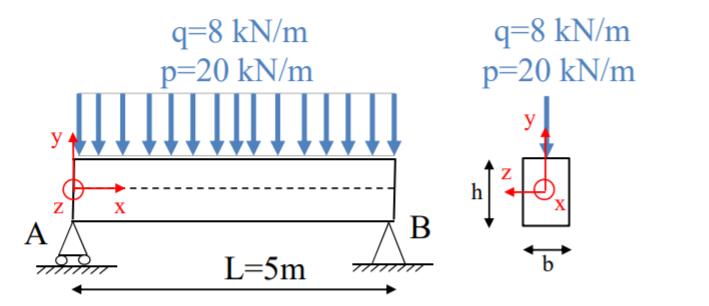
On considère une poutre en bois soumise à deux charges réparties verticales : une charge permanente p de 20 kN/m et une surcharge d'exploitation q de 8 kN/m entre A et B. La longueur de la poutre est de 5m. La section est rectangulaire et a pour largeur b et pour hauteur h.
Tous les calculs seront effectués à l'ELU
Question 1. Calculer la charge répartie totale à l'ELU, on rappelle que la combinaison à l'ELU est : 1,35G + 1,5Q où G correspond aux charges permanentes et Q aux surcharges d'exploitation.
Déterminer la valeur maximale de l'effort tranchant et préciser où elle est atteinte.
Question 2. La contrainte limite de cisaillement pour le bois est ̅= 3. Si l'on considère
que la largeur de la poutre est constante et vaut b=0,15m, calculer la hauteur minimum hmin pourvérifier le critère de résistance au cisaillement. On arrondira hmin au dixième supérieur.
Question 3. La poutre est maintenant dimensionnée. En considérant que le poids volumique dubois est de 5,15 kN/m3, vérifier le critère de résistance au cisaillement en prenant en compte le poids propre.
Pour la première question, j'ai calculé la charge répartie totale à l'ELU :
1.35G+1.5Q = 1.35*20+1.5*8 = 39 kN/m = I
Ainsi je trouve pour les résultantes :
Xb = 0
Ya = I.L/2
Yb = I.L/2
J'ai ensuite déterminer le torseur de cohésion à droite et je trouve pour l'effort tranchant:
Ty = I.L/2 - I.(L-x)
Malheureusement j'ai peur de m'être trompé dans mes résultats et si j'ai le droit ou non de faire la somme des surcharges d'exploitations avec les charges permanentes pour trouver l'effort tranchant.
Merci de l'aide.
Bonsoir ShowTake,
Tu as fini de réviser tes autres matières à ce que je vois 
.
Première question ELU = ?
combinaison à l'ELU est : 1,35G + 1,5Q où G correspond aux charges permanentes et Q aux surcharges d'exploitation.
Si je comprends bien, on a une relation qui permet de déterminer une charge répartie équivalente le long de la poutre ?
Bonjour gbm,
Oui j'ai fini mes révisions ahah
L'ELU c'est l'état limite ultime de la poutre. Oui, la relation permet de déterminer une charge répartie équivalente le long de la poutre normalement.
Merci pour les explications.
Déjà, pour ce qui est de la première étape, un petit schéma s'impose :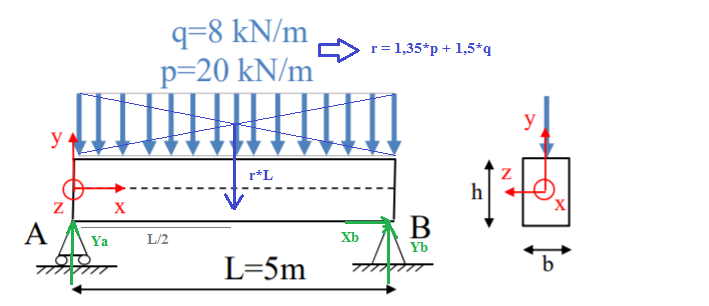
J'ai changé ta notation "I" par "r" dans la mesure où "I" est la notation usuelle pour le moment quadratique.
Déterminons donc les efforts aux appuis :
* Equation de la résultante statique /x :
* Equation de la résultante statique /y :
* Equation de moment en A /z :
Et donc
=> on retrouve bien la même chose.
J'arrive pour l'effort tranchant
Nouveau schéma pour la détermination de l'effort tranchant :
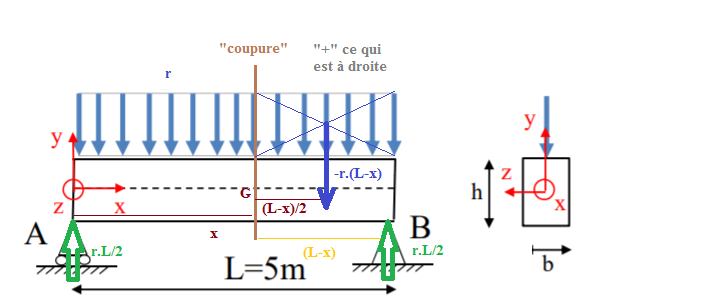
Si je regarde à droite de la section (étant donné que la poutre est symétrique, cela ne simplifie pas le calcul de regarder à gauche ou à droite) :
Parfait, alors. Mais du coup si on étudie la fonction de l'effort tranchant.
Ty' = r
Du coup la fonction est strictement croissante sur [0;L]
Du coup l'effort tranchant serait maximale en L donc en 5 ?
Si on regarde le diagramme de l'effort tranchant c'est correct, mais attention au signe (tu raisonnes trop mathématique ) :
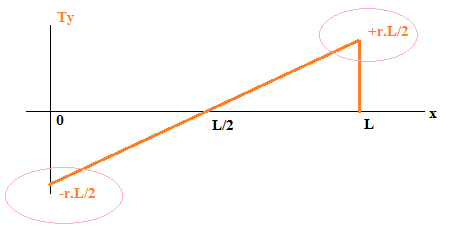
Mmh, mais du coup nous sommes d'accord que l'effort tranchant est atteinte pour x = L = 5 et sa valeur est Ty(L) = r.L/2 = 39.5/2 = 195/2 = 97.5 kN ?
D'accord parfait, merci à vous
Je vais vous laisser ici pour ce soir, en vous souhaitant une bonne soirée. Je reviendrai vers vous pour la suite demain.
Bonjour,
Du coup pour la question 2. Sachant que la formule de contrainte au cisaillement est:
avec V l'effort tranchant maximum et Av l'aire de la section.
Alors :
Sachant que bmin = 0.15m = 15 cm
Alors 325/15 = 21.7 cm si on arrondi à la dixième supérieur.
Selon vous est-ce bon ?
Oui c'est exactement ça : en première approche, on peut écrire la contrainte de cisaillement de la façon suivante :
Ton raisonnement me semble donc correct
Oui c'est exactement ça : en première approche, on peut écrire la contrainte de cisaillement de la façon suivante :
Ton raisonnement me semble donc correct
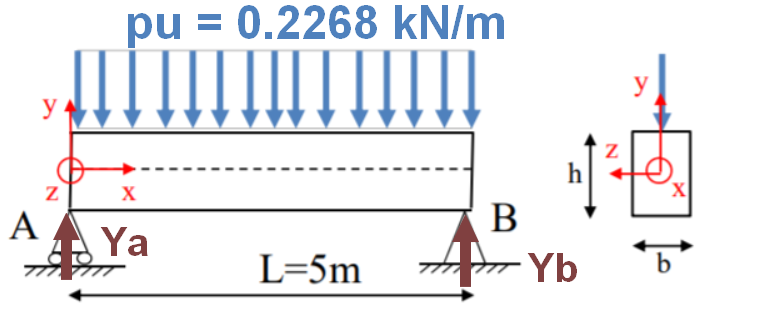
Parfait alors cependant je n'arrive pas à remontrer le critère de cisaillement à partir du poids propre. Je me suis dis que j'allais recalculé l'effort tranchant:
Donc 5.15*0.217*0.15 = 0.168 kN/m
Charge à l'ELU : 0.168*1.35 = 0.2268 kN/m
Mais après je ne vois pas comment faire :/
Donc désormais on ne considère plus que la poutre soumise qu'à son propre poids ?
Si oui, te souviens-tu de la méthode avec laquelle on avait déterminé le poids réparti à une abscisse x donnée (exercice avec la poutre encastrée) ?
Il va falloir s'en inspirer en recalculant dans un premier temps les efforts aux appuis puis en faisant la même illustration graphique que proposées dans le dernier exercice.
Je remets la question : "Question 3. La poutre est maintenant dimensionnée. En considérant que le poids volumique dubois est de 5,15 kN/m3, vérifier le critère de résistance au cisaillement en prenant en compte le poids propre."
Oui nous avions utilisé les théorème de Thalès et Pythagore mais ici nous n'avons pas un encastrement mais des réactions d'appuis simple je ne vois donc pas le schéma pour trouver p(x) 
Commence par faire un schéma de la situation avec la poutre sur les deux appuis et soumise à son propre poids.
Etape 1 : on détermine les réactions aux appuis
Etant donné qu'on reste sur une répartition uniforme sur une poutre à 2 appui, ça ne change pas effectivement, si ce n'est que "p" n'a pas la même valeur.
Tu n'avais pas l'air d'en être convaincu
Du coup sachant que Ty = -pu.(L-x)+pu.L/2 et que x est maximum en L. Alors Ty = pu.L/2
Ty = 0.2268*5/2 = 0.567 kN
On remplace dans la formule = 0.567/0.0325 = 17.44 MPA
Êtes-vous d'accord avec moi ?
Le raisonnement est correct, tu as bien fait attention de mettre les données dans les unités SI (kN en N et S en m²) ?
Non, l'unité de la pression (Pa) est homogène (N/m²)
Tau = 0,2268.103/0,0325 = 6,979 kPa
Oui mais du coup on a un problème car "La contrainte limite de cisaillement pour le bois est = 3 MPA"
Comme on trouve une valeur bien inférieure à la contrainte limite (au coefficient de sécurité éventuel près), tu as donc une poutre bien dimensionnée pour son propre poids
Ah d'accord, pardonnez-moi il est vrai qu'il fallait trouver en dessous et non au dessus. Vous avez donc raison. Je vous remercie pour l'aide que vous m'avez apporté Je reviendrai surement vers vous pour d'autre exercice plus tard au vu de ma composition de maths je pars réviser un peu. En vous remerciant à bientôt
Annuler
connectez vous