Inscription / Connexion Nouveau Sujet
rdm
Bonjour,
J'ai un exercice dont je n'arrive pas à trouver une solution surtout au niveau de la
détermination de la section je ne suis pas sûr de ce que je fais..
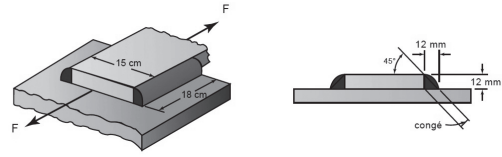
Voici l'énoncé de l'exercice et la figure :
Pour réunir deux plaques, on utilise souvent des soudures d'angle. On demande de calculer la force de traction maximale admissible en sachant que l'acier utilisé est en S235 et que l'on se fixe une sécurité de 3.
Je cite ce que j'ai fait :
Pour calculer la force de traction je dois calculer la section S ,puis j'applique cette relation : F/S ≤ Re/s ; avec Re= 235 Mpa et s=3 (depuis l'énoncé)
Et pour la section S voilà ce que j'ai fait :
S=Surface de rectangle + Surface de demi-cercle (quart de cercle de soudure + quart de cercle de soudure= demi cercle )
/J'ai travailler dans la vue de face de la pièce (la figure à droite)/
Alors : S=(150*12)+(3.14*12²/2)
je ne suis pas sûr de ce calcul ..
Qu'en pensez-vous ?
Merci d'avance .
Bonjour,
Il faut que tu prennes le temps d'expliquer ce que tu fais avec des mots, ta pensée n'est pas très claire en l'état. N'oublie pas que le jour d'un examen ou d'un concours, la qualité rédactionnelle compte tout autant que le résultat final.
Ici, tu as déjà une première chose à préciser : on applique le principe des actions réciproques : l'effort généré via la contrainte de cisaillement sera égale à la force de traction exercée sur la plaque soudée sur la première.
Il y a donc une première condition liée au cisaillement à exprimer.
Ensuite, je ne comprends pas ce que tu as cherché à faire pour le calcul de "S".

Merci pour ta réponse,
Alors, je cherche S (l'aire de la pièce à expanser) pour que j'applique la condition de
résistance suivante pour trouver la force F de traction demandée : F/S ≤ Re/s
OK,
S = 0,15*0,18 (aire du rectangle) + 0,18*0,012*2 (aire des deux petits rectangles dus aux soudure) = ... m²

Je vois qu'il ne s'agit pas d'un rectangle de soudure mais d'une quart de cercle parce que
c'est mentionné à l'énoncé "soudure d'angle" ce qui montre qu'il s'agit d'une cercle
et pas rectangle.
Attention, la section de la soudure qui nous intéresse est celle qui subit le cisaillement, donc la section longitudinale (rectangle 18 cm x 12 mm) et non pas la section transversale (= 1/4 de cercle).

ça veut dire qu'on va faire l'aire du cylindre ?
Si on considère les morceaux à droite et à gauche de soudure forment la moitié d'un
cylindre on fait : S=2*3.14*12*180/2 mm² \Leftrightarrow S=3.14*12*180 mm²
?
Bonjour,
Oui, étant donné qu'on a un demi-cylindre de part et autre de la plaque, cela correspond à l'air projeté d'un cylindre complet.



