Inscription / Connexion Nouveau Sujet
Rangée nodale
Bonsoir,
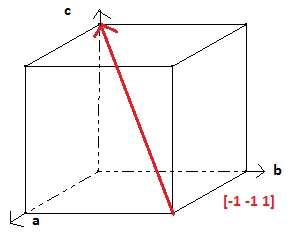
Je pensais avoir compris les indices de Miller concernant les plans et rangées, mais je tombe sur un cas que je ne saisis pas. Sur la figure ci-jointe, la rangée dessinée (diagonale dans le cube) a pour indice [-1 -1 1]. Pourquoi donc? Jusque là, je raisonnais pour trouver ces indices avec les axes a, b, et c que coupait la rangée, puis en prenant l'inverse, etc... Pouvez-vous m'expliquer ce cas-là svp?
Merci d'avance!
Bonjour,
C'est cela puis que sur a vous passez de 1 à 0 ainsi qu'en b alors que pour c de 0 à 1
Soit :
(0,0,1)-(1,1,0)= (-1,-1,1)
Petit complément.
http://fr.wikipedia.org/wiki/Indices_de_Miller_et_indices_de_direction#Rep.C3.A9rage_d.27une_direction
Cordialement,
Benjamin
Je ne comprends pas trop votre explication.. En effet, on m'a dit qu'il fallait simplement regarder en quels points la rangée intercepte les vecteurs de base; or ici, la rangée ne coupe ni a, ni b! Pour c je suis d'accord, puisqu'elle le coupe en 1, soit 1/1=1... non?
Bonjour,
Oui désolé je me suis mal exprimé, je suis allé un peu vite, le temps me fait défaut ces temps-ci.
Si l'on note ,
et
les vecteurs de la base, alors les indices de direction [uvw] correspondent au vecteur
cf : wikipedia.
On peut traiter cela de la même manière qu'un vecteur
Cordialement,
Benjamin



