Bonjour
Sans schéma, difficile d'être catégorique. Il semble bien que ton énoncé considère que l'ensemble du dispositif (tige initialement horizontale correspondant à l'axe (Ox) et tige verticale portant le point d'attache R du ressort) tourne de l'angle . Cette hypothèse est cohérente avec les calculs faits. Sinon (axe (Ox) tournant de et tige (OR) restant verticale), la longueur L du ressort vérifierait :


Cela rendrait, à mon avis, le problème inutilement "calculatoire".
Sous toutes réserves...

Bonsoir,

Je m'excuse pour ma réponse tardive. En fait, même dans le corrigé il n'y a pas de schéma, ni une indication de plus. Peut-être comme vous avez dit il a été considéré que tout le système tourne d'un angle . De toute façon le problème resterait calculatoire je pense, parce que même dans le cas où tout le système a tourné, on ne ferait que d'autres calculs pour faire des conclusions sur les positions d'équilibre et les changements par rapport à la première situation.

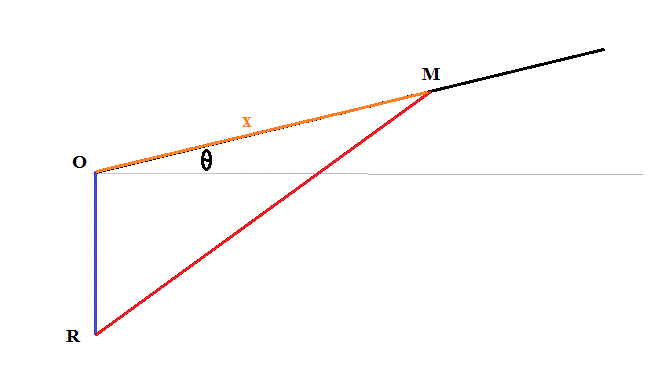
RM² = OR² + OM² - 2.OR.RM.cos(90° + theta)

RM² = L² + x² - 2.L.x.cos(90° + theta)

RM² = L² + x² + 2L.x.sin(theta)

Longueur du ressort =



En considérant nulle l'énergie potentielle élastique (Ee) du ressort non contraint, on a :



En prenant O comme niveau de réference pour les Epp nulles, on a :

Epp = m .g. x.sin(theta)

Et donc l'énergie potentielle de l'ensemble masse + ressort est :



Et si on a theta = 0, alors,
-----
Remarque :

Comme l'énergie potentielle est définie à une constante près, si on préfère travailler avec une Ep = 0 pour x = 0, on peut si on le veut "décaler" mes solutions d''un terme constant (qui serait = - 1/2.k.(L - Lo)²)...

Sauf distraction.  

Complément à ma réponse :

Comme, il est précisé que theta est "petit", il est possible que l'auteur ait supposé négligeable le terme 2Lx.sin(theta) par rapport à L²+x².

... cela peut être légitime, mais devrait alors être clairement indiqué.

Bonjour EvDavid
Deux remarques complémentaires valides en supposant que la tige OR reste verticale quand la tige (Ox) tourne de l'angle .
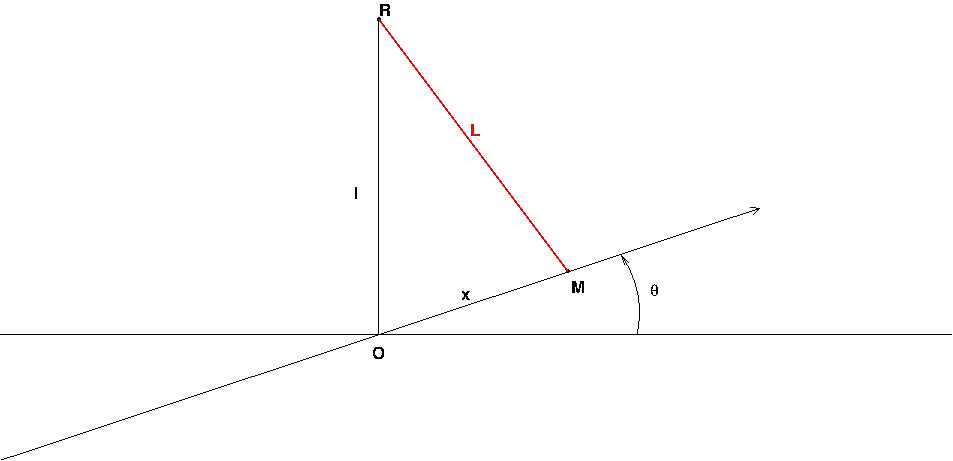
1° : la plupart des problèmes de ce type suppose le point R au-dessus du point O. Le théorème d'Al-Kashi conduit directement à l'expression de L² que j'ai indiquée dans mon message du 26-07-18 à 10:35. Bien sûr, puisque aucun schéma n'est fournie, rien n'empêche d'imaginer le point R en dessous du point O, le même théorème conduisant alors à inverser le signe du sinus.
2° : on peut aussi réfléchir sur la possibilité de négliger le terme en 2l.x.sin() devant x², ce qui reviendrait à considérer :
|x|>>2l.sin().
Ce genre de problème consiste en général à étudier les positions d'équilibre, leur nature stable ou instable puis les oscillations de faible amplitude autour de la position d'équilibre stable. Autrement dit, l'approximation envisagée ne peut être légitime que si la position d'équilibre stable d'abscisse x_e vérifie :
|x_e|>>2l.sin().
L'étude littérale de la dérivée par rapport à x de Ep avec détermination des valeurs littérales des "zéros" de cette dérivée, est longue et délicate. Je préfère raisonner sur quelques cas simples en conservant l'expression de L² que je t'ai fournie.
a) premier cas simple : le ressort est très raide (k élevé) de sorte qu'une position d'équilibre corresponde à l'axe (RM) du ressort sensiblement perpendiculaire à la tige (Ox). Cette situation correspond à :
x_el.sin()
Avec R en dessous de O, on trouverait : x_e-l.sin(). On voit clairement que l'approximation envisagée n'est pas possible.
b) autre cas simple : sans faire de calculs, on voit bien physiquement qu'il serait possible d'ajuster les valeurs de k,l et l_o de façon que l'action du ressort compense exactement la composante du poids selon (Ox) ; dans le cas particulier x_e=0. L'approximation serait là aussi évidemment fausse !
c) on peut aussi envisager la situation d'un ressort très peu raide (k assez faible), l'équilibre stable correspond à une valeur x_e <0. En posant :


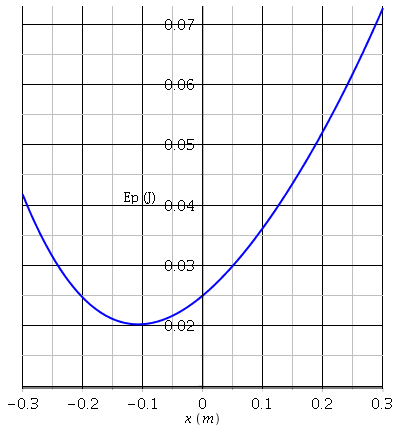
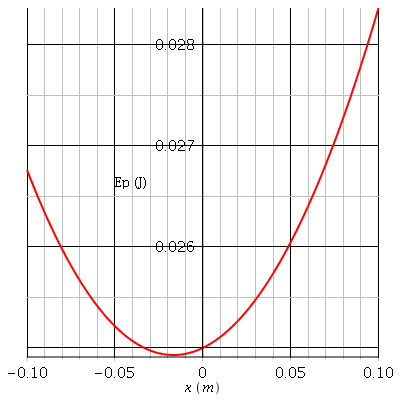
On obtient la courbe Ep=f(x) ci-dessous (courbe bleue) pour les valeurs numériques suivantes :
l_o=0.90m ; l=1,0m ; m=0.10kg ; k=5,0N/m ; =10° .
On obtient une position d'équilibre stable pour :
x_e-11cm.
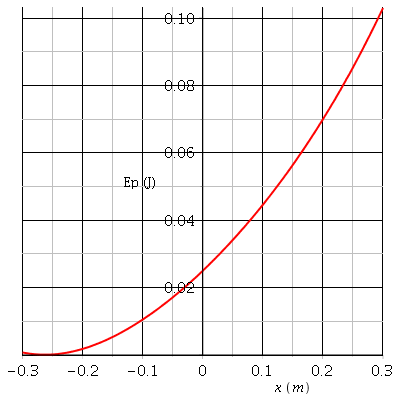
Facile de vérifier là encore que l'approximation n'est pas possible. On peut aussi s'en assurer en traçant la courbe Ep₁=f₁(x), en enlevant de l'expression de Ep le terme en 2l.x.sin(). On obtient des résultats très différents (courbe rouge).
Bref : on en revient à la conclusion de mon précédent message : si on veut conserver l'expression de l'énergie potentielle des questions précédentes, il faut imaginer une rotation globale du dispositif.

Si l'angle theta est comme je l'ai dessiné, la formule donnant la longueur du ressort est celle que j'ai indiquée.

En poussant la valeur de theta, c'est évident. Par exemple avec L = x et theta = 90°, la longueur du ressort serait 2x (comme on l'aurait avec ma formule) et ne vaudrait évidemment pas 0.

Evidemment, si on incline la barre dans l'autre sens (par rapport à mon dessin), alors il y aurait un changement de signe dans ma formule. On ne peut pas deviner à partir de l'énoncé tel qu'il a été donné.

Si c'est l'ensemble qui tourne de l'angle theta (et pas seulement la barre) ... alors il fallait l'écrire explicitement dans l'énoncé. (qui, quoi qu'il en soit est mal foutu).

Je pensais avoir été clair en expliquant que je considérais, comme cela se fait le plus souvent dans ce type de problème, le point R au-dessus du point O en précisant aussi que, en absence de précision de l'énoncé, placer R au-dessous de O est un choix possible.
Quoi qu'il en soit, voici, pour plus de clarté, le schéma correspondant aux calculs de que j'ai faits.
Bien sûr que l'énoncé, tel qu'il a été présenté sur ce forum, n'est pas précis. J'ai simplement expliqué qu'il n'est pas possible, en absence de rotation globale du dispositif, de conserver l'expression antérieure de l'énergie potentielle élastique du ressort. Le terme en 2l.x.sin() n'est pas d'influence négligeable.

Et alors ?

L'énoncé étant ce qu'il est (mal foutu), toutes les interprétations sont possibles.

J'ai donné la mienne qui vaut bien n'importe quelle autre.

N'importe quoi.

L'énoncé est tellement plein de lacunes que tout est permis comme supposition.

Et ce que j'ai écrit n'est évidemment pas "physiquement faux".

Il faut bien entendu envisager les cas numériques concrets possibles dans l'esprit de l'auteur... qu'on ne connait évidemment pas ici, pour juger si ou peut ou non négliger "quelque chose" devant 'une autre chose".... et donc cela "PEUT être légitime", à ne pas confondre avec "C'est légitime".

Dans mon message du 28-07-18 à 15:11 j'ai montré (cas a) que , lorsque le ressort a une raideur élevée, un raisonnement littéral montre que, pour x égal ou voisin de la valeur à l'équilibre x_e, nous avons, pour sin() non nul :
2.l.x.sin()2x²
Nous sommes très très loin de la situation 2.l.|x|.sin()<<x²
Il faut bien comprendre que diminuer sin() diminue aussi x et x² au voisinage des positions d'équilibre. Donc sin() très petit n'implique pas 2.l.|x|.sin()<<x².
Pour les autres situations, il est vrai que je me suis contenté de simulations numériques. Obtenir l'expression littérale de x_e est très compliqué !
Cela dit : si JP peut fournir un jeu de valeurs numériques réalistes (valeurs qui permettent au ressort de rester dans son domaine élastique) telles que :
2.l.|x_e|.sin()<<x_e²
je serais ravi d'avoir tort ! Je suis quelqu'un qui reconnais de bonne foi ses erreurs !

Je n'ai jamais écrit 2.l.|x|.sin(theta) < < x², mais, bien : il est possible que : 2.l.|x|.sin(theta) < < x² + l²

c'est fondamentalement différent.

Exemple numérique :

L = 1 m et x dans [-0,1 ; 0,1] et theta = 1°

2.l.|x|.sin(theta) < < x² + l² revient à :

0,035 |x| < < x² + 1 ce qui est vrai pour tout x dans [-0,1 ; 0,1]

Mais aussi :
0,035|x|<<l !
enfin...
Pour négliger un terme dans une somme de trois termes, il faut que le terme que l'on se propose de négliger soit très inférieur à chacun des deux autres...
Sinon, à ce compte là, puisque, dans tous les cas que j'ai testé (j'ai reconnu ne pas avoir fait une étude générale...), la valeur absolue de 2l.x.sin() est supérieure ou du même ordre que x², pourquoi ne pas supprimer aussi x², ce qui conduirait à une énergie potentielle du ressort indépendante de x ?
Puisque l'énergie potentielle se définit à une constante près. On pourrait supprimer cette constante et faire comme si le ressort n'existait pas. Resterait la masse sur un plan incliné...

Les valeurs numériques prise dans le messages précédents ne correspondent pas à une simulation d'un dispositif... Je viens de tester l'hypothèse d'un angle égal à 1° en conservant les autres valeurs numériques précisées dans mon message du 28-07-18 à 15:11.
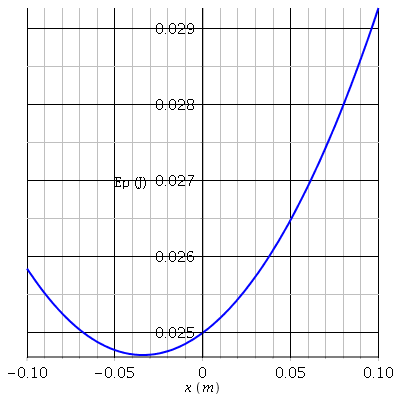
En tenant compte du terme en 2l.x.sin() ( voir courbe rouge) on obtient une position d'équilibre stable pour x_e=-1,66cm (et oui : comme déjà expliqué : diminuer sin() conduit à une diminution de |x_e| mais aussi de x_e²)
En négligeant le terme en 2l.x.sin() tout en conservant le terme en x² (voir courbe bleue), on obtient x_e=-3,41cm ; on commet ainsi sur x_e une erreur relative de 105% : une paille !
Bref : en guise de conclusion car, en ce qui me concerne, je pense avoir épuisé le sujet :
Une évidence : l'énoncé tel qu'il a été fourni au forum est imprécis. Dans ces conditions, il n'est pas interdit, par curiosité intellectuelle, d'imaginer des améliorations à l'énoncé susceptible de le rendre cohérent.
1ère possibilité : en envisage une rotation globale du dispositif de l'angle . Cela a l'avantage de conserver l'expression précédente de l'énergie potentielle élastique, le problème reste raisonnablement "calculatoire".
2ème possiblité : seul l'axe (Ox) tourne, la tige (OR) reste fixe. Cela introduit un terme supplémentaire dans l'expression de la longueur du ressort qui, sauf cas très particuliers éventuels que je n'ai pas réussis à caractériser, n'est absolument pas négligeable. Cette situation ne parait bien compliquée à étudier...

N'importe quoi.

Comme souvent, vanoise argumente à coté du sujet.

Le but était bien d'estimer la variation d'énergie potentielle en inclinant un peu la barre par rapport à sa position horizontale du départ.

Et à partir de là, la question s'est posée de savoir si on pouvait où non négliger la variation du terme de l'énergie élastique.

Et évidemment, cela dépend des valeurs numériques des données.

Je change des valeurs, en prenant k 3 fois plus petit et m 3 fois plus grande, et on regardant le problème posé et pas un autre ...

En ordonnées : le delta Ep (en J) entre theta = 0 et theta = 1° et en ordonnées les x (en m)

On a ceci (pas vérifié)



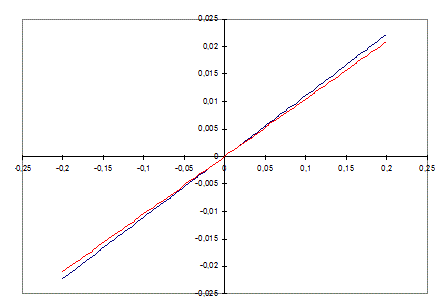
Les 2 courbes correspondent, l'une en tenant compte des variations des 2 termes (E élastique et Epp) et l'autre en négligeant l'effet de la variation de E élastique.

On voit que (AVEC CES VALEURS NUMERIQUES) l'erreur faite en négligeant l'effet de la variation de l'énergie élastique du ressort sur la différence de Ep due à un petit angle est petite ... et peut "peut-être" être négligée.

Et évidemment, on peut toujours trouver des valeurs numériques où l'erreur faite serait trop grande et donc inacceptable ... d'où le "peut être".

Je m'arrète aussi sur le sujet.