Bonjour,

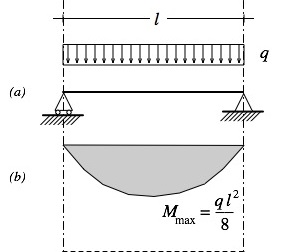
J'ai une question hyper simple concernant la poutre sur cette photo.
Elle est symétrique, de longueur l, avec une charge répartie p.

Pourtant, je n'arrive absolument pas à comprendre pourquoi le moment de flexion maximal est pl²/8 ; personnellement je trouve sans cesse 3pl²/8.

Je dis que : M(x)= Ra*x - p*x*(x/2)
       donc  M(x)= (pl/2)x - px²/2

Comme elle est symétrique, le moment maximal se trouvera en l/2.

En remplaçant donc dans l'équation, j'obtiens :

M(l/2)= (pl/2)*(l/2) - p*(l/2)²/2
M(l/2)= pl²/4 - pl²/8
M(l/2)= 4pl²/8 - pl²/8
M(l/2)= 3pl²/8

Mais avec les applications numériques, mon résultat est faux.

Pourriez-vous m'aidez svp ?
Pas moyen de voir mon erreur.