Bonjour
Il faudrait un énoncé complet pour être sûr mais en général  , aux pulsations de coupure, H =Hmax/2

l'exercice et comme suit :
1. Montrer qualitativement la nature du filtre.
2. Donner l'expression de la fonction de transfert ; H( jw )
3. Donner l'expression de la pulsation propre w0
de ce filtre, ainsi que le facteur
d'amortissement m.
4. Exprimer le gain G et la phase phi en fonction de la fréquence.
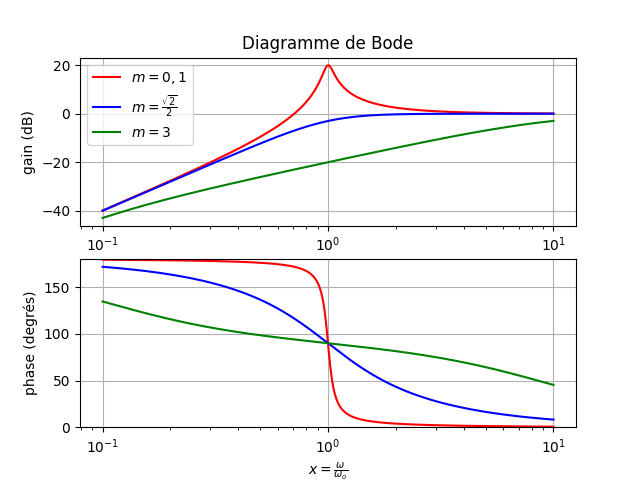
5. Pour quelle valeur de w le gain est-il maximal en fonction de m? En déduire la (ou les)
pulsation(s) de coupure à -3dB.
je trouve w_max=w₀(1/1-2m²)
En fait je sais que aux pulsations de coupure H =Hmax/2, mais y-a t il une façon de la déduire à partir de ce w_max?

merci

Tu as oublié la racine carrée de 2.
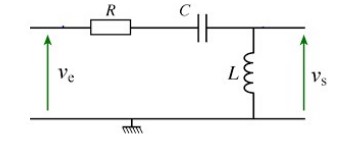
Si tu scannais le circuit et indiquais les résultats déjà obtenus  ?

Je trouve la fonction de transfert d'un filtre passe haut
wmax=w0(1/1-2m2) mais comment je peux déduire le w du coupure à partir de ça. Je peux faire remplacer le w_max trouvé dans le module du fonction du transfert, mais ça me semble très long et prend du temps.

Tu as besoin de déterminer Hmax. Pour cela, il faut distinguer deux cas selon les valeurs de m, selon qu'il y a résonance possible ou pas. Cela conduit soit à une, soit à deux pulsations de coupures.

Pouvez-vous m'expliquer plus s'il vous plaît, je me suis perdu dans ces formules

Pour ne pas avoir de calculs fastidieux de dérivée à effectuer, tu as tout intérêt à écrire la fonction de transfert avec une constante au numérateur. Je résume les calculs en passant certains intermédiaires... Tu pars de :

  avec  :   et    et  

On divise tous les termes par (-x²) :



Tu peux remarquer que la fonction de transfert se déduit de celle du passe-bas du second ordre en remplaçant (jx) par 1/(jx); On passe au module :

en posant :



Inutile donc de se fatiguer à calculer la dérivée de H par rapport à x. Il suffit de s'intéresser aux variations en fonction de Y de P(Y). Tu vas être amené à distinguer deux cas :

1° : : la dérivée de P(Y) par rapport à Y est constamment positive quel que soit Y donc quel que soit x : H fonction monotone décroissante de Y donc fonction monotone croissante de x ; pas de résonance. H_max=1; Il suffit donc, pour obtenir les pulsations de coupures, de trouver les valeurs de Y puis de x pour lesquelles P(Y)=2.

2° : : la dérivée de P(Y) s'annule pour une valeur particulière de Y donc une valeur particulière de x à déterminer. En déduire l'expression de P_minimum. Les pulsations de coupure correspondront à P(Y)=2P_minimum.

Ce diagramme réalisé pour trois valeurs de m différentes t'aidera peut-être.

Merci infiniment monsieur pour l'aide
merci bien pour votre temps