Inscription / Connexion Nouveau Sujet
Puissances et résistance dans un circuit.
Bonjour ,
Merci d'avance. 
On monte en série entre les bornes d'un générateur fournissant une tension sinusoidal de pulsation , les dipoles suivants :
- une bobine (L1, R1) de bornes A et B d'impédance Z1 ;
-un conducteur ohmique R de bornes B et C.
L'intensite instantanée du courant du circuit est (en A) : .
Un voltmètre de grande impédance successivement placé entre A et B, puis entre B et C et enfin entre A et C indique les valeurs efficaces suivantes : UAB = 45 V ; UBC = 40 V ; UAC = 75 V.
La résistance du conducteur ohmique est courant.
On note la phase de la tension entre les bornes A et B par rapport a l'intensité du courant.
1) Exprimer en fonction de Z1 , R2 , Im , t et les tensions instantanées uAB et uBC.
2) Écrire la relation entre les tensions instantanées uAB , uBC et uAC.
3)
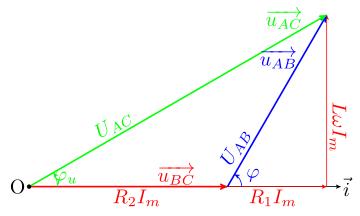
3-1) Faire la construction de Fresnel.
3-2) Montrer que la phase vérifie la relation
4) Déterminer :
4-1) la puissance consommée dans le conducteur ohmique ;
4-2) la puissance consommée dans la bobine ;
4-3) la résistance de la bobine.
Réponses
1) * avec
*
Bonjour
Je t'ai aidé il y a peu sur un exercice analogue utilisant les vecteurs de Fresnel. Il faut s'en inspirer car tu as écrit de nombreuses choses fausses.
Circuit RLC.
Il n'y a pas de condensateur ici ! Le diagramme de Fresnel t'a été fourni. Je le recopie en te laissant adapter les notations.
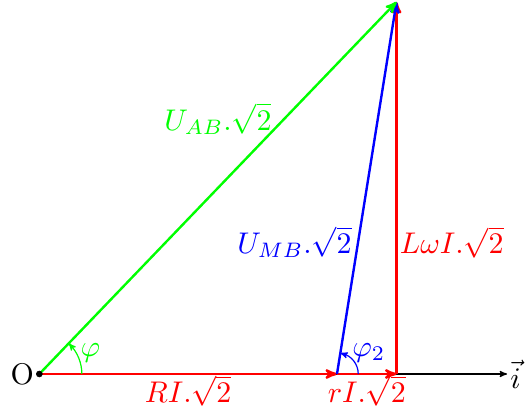
Le schéma que tu fournis ne contient pas de condensateur. Le problème est très analogue à celui traité récemment où le circuit était constitué d'une bobine en série avec une résistance. Seuls les notations changent.
Si je peux me permettre : au lieu d'accumuler une succession d'exercices qui t'embrouillent plus qu'autre chose dans la mesure où les notations et les conventions changent de l'un à l'autre, tu ferais bien d'étudier de façon approfondie le cours et quelques exercices types.
Oui , je vois. Mais je maîtrise parfaitement mon cours.
Et j'ai pu faire l'autre exo sans soucis , pourtant je ne vois pas vraiment de lien avec celui-ci.
Et là il s'agit d'un DM.
Alors
D'après le diagramme de Fresnel,
Donc
1°. J'utilise les données de l'énoncé en supposant que la résistance de 20
correspond à R1. Ces formules sont générales. Je les rappelle pour bien fixer les notations. Il faut bien faire la différence entre valeurs instantanées, valeur efficaces et valeurs maximales
avec : UBC=R2.I (I : valeur efficace de i(t))
2°. Les lois obtenues en régime continu s'appliquent en régime sinusoïdales aux valeurs instantanées (attention : elles ne s'appliquent pas au valeurs efficaces et aux valeurs maximales).
3°. Je te fournis à nouveau le diagramme de Fresnel après avoir adapté les notations à celle de ce problème.
Pour 3.2 : penser au théorème d'Al Kashi.
Annuler
connectez vous