Bonjour
Le problème est équivalent à imaginer l'aimant fixe et la bobine se déplaçant par rapport à lui à la vitesse . Je te donne deux pistes de réflexion.
La première consiste à raisonner sur le flux du champ B à travers la bobine. La bobine se comporte au cours du mouvement relatif comme un générateur de force électromotrice :


Pour déterminer l'intensité i à travers la bobine, il faut savoir à quoi est reliée la bobine pour fermer le circuit. Très souvent dans ce type de situation, il est possible de négliger  le phénomène d'auto-induction par rapport au phénomène d'induction (hypothèse à vérifier). Si la bobine de résistance Rb est fermée sur elle-même,  l'intensité à travers la bobine vaut :


la puissance instantanée produite par induction est :

Tu peux calculer aussi l'énergie fournie à l'extérieur au cours du mouvement :


Cette méthode a l'avantage de ne faire intervenir que des notions à ton programme mais ne sera pas simple à mettre en oeuvre : pas facile de connaître la valeur de B dans l'aimant pour calculer le flux à travers la bobine.
Une seconde méthode me paraît plus prometteuse même si, je crois, elle a disparu du programme de certaines filières de CPGE. Pour simplifier, je suppose que l'aimant est un barreau cylindrique. Dans ces conditions, le problème est à symétrie cylindrique, on peut travailler dans un repère cylindro-polaire et écrire que B à l'extérieur de l'aimant a pour expression générale :


Si v désigne la vitesse de la bobine par rapport à l'aimant, il est facile de montrer en utilisant la loi de Lorentz que, du point de vue de électromagnétique, tout se passe comme si la bobine était immobile, chaque point de la bobine étant dans un champ électrique de vecteur E :


La force électromotrice induite se calcule alors comme la circulation du vecteur E le long de la bobine. Si celle-ci est assimilable à N spires identiques de rayon moyen R, le calcul est simple... Ayant e, tu obtiens la puissance comme précédemment. Cette méthode a l'avantage de ne faire intervenir que la composante radiale du vecteur B à l'extérieur de l'aimant.
Cette composante peut être mesurée à l'aide d'un teslamètre en différents points à la distance r=R de l'axe de l'aimant pour différentes cotes z.  
Si par hasard, l'aimant est de dimensions suffisamment petites devant le rayon moyen R , on peut établir l'expression théorique de Br en assimilant l'aimant à un dipôle magnétique...
Je te laisse réfléchir à tout cela... N'hésite pas à poser d'autres questions si tu le juges utile.

Merci

Bonjour,

Je veux essayer la première option que vous me donnez.

J'ai plusieurs questions.

Pour le calcul du flux de B, phi = int(B.dS), mais qu'est ce que dS? l'aire formée par le diamètre de la bobine?

Ensuite, pour calculer le champ B d'un aimant cylindrique, j'ai trouvé une relation sur le site . Je ne comprends pas bien ce que représente z, peut-être est-ce la distance entre la surface de l'aimant et le bout de la bobine? C'est la seule grandeur qui dépendrait du temps.

Sur le site j'ai trouvé des informations sur le champ rémanent de plusieurs aimants. J'ai choisi un aimant au néodyme car il fait partie des aimants les plus puissants N52 avec Br = 1.45T environ.

J'ai dimensionné ma bobine et mon aimant en laissant en entrefer 1 mm. Mon aimant a une hauteur D = 80 mm et un rayon R = 15 mm pour éviter l'arc-boutement comme le préconise le site http://stigmpicasso.free.fr/COURS/terminale/translation/translationprof.pdf qui dit que : D>2*R * 2.5

Merci de votre aide.

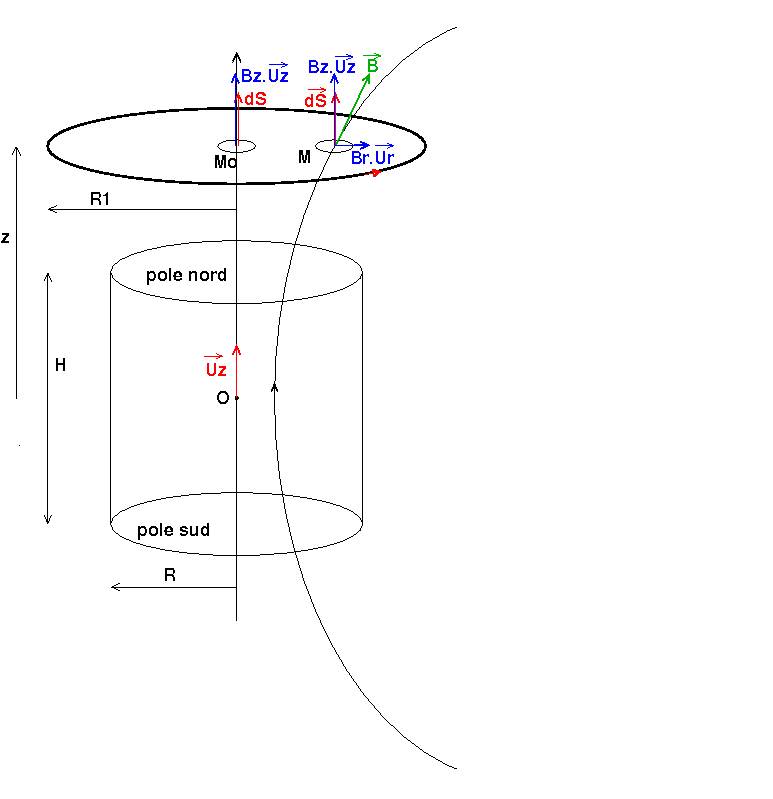
J'ai repris la description de l'aimant cylindrique décrit sur le site que tu as indiqué. Je change un peu les notations car celles fournies sont vraiment piégeantes. Je note O son centre , (O,Uz) son axe de symétrie, R son rayon et H sa hauteur. Le vecteur champ d'induction magnétique en un point quelconque Mo de cote z, sur cet axe de symétrie a pour expression :


Il s'agit de la formule fournie sur le site mais adaptée pour tenir compte du changement de notation et surtout du changement d'origine des cotes. Avec mes notations, z=0 correspond au centre O alors que sur le site, z= 0 correspond au pole nord de l'aimant. Avantage pour la suite : Bz apparaît ainsi comme une fonction paire de la variable z, ce qui peut simplifier certains calculs ultérieurs...
J'assimile la bobine plate à un ensemble de N spires identiques de rayon R1, d'axe (O,Uz), de centre Mo. Il s'agit de calculer le flux du vecteur B créé par l'aimant à travers le disque délimité par les spires. Les spires étant orientées conformément au schéma ( flèche rouge), en chaque point M du disque, on peut définir un petit élément de surface caractérisée par le vecteur dS normal au disque et de norme égale à l'aire de la surface élémentaire :
Le vecteur champ d'induction magnétique en M a deux composantes : une composante radiale et une composante suivant Uz : .
Le flux élémentaire à travers la surface élémentaire centrée en M est :


Coup de chance (je te ferais plus tard la démonstration si tu le juges nécessaire) : Bz en M garde sensiblement la même valeur qu'en Mo tant que la distance de M à Mo ne dépasse pas R.
En pratique, si le rayon R1 de la bobine en translation n'est que de très peu supérieur à R (écart relatif de 10% au plus) on peut écrire que le flux à travers la bobine plate est en bonne approximation :


Le fait de choisir R dans le calcul de l'aire du disque plutôt que R1 compense à peu près dans le calcul du flux le fait que Bz diminue lentement en fonction de la distance de Mo à M...
Si tu connais le mouvement de la bobine plate par rapport à la bobine, la loi z = f(t) est connue, on obtient le flux en fonction du temps puis la fém induite...
Attention : si R1 est nettement supérieur à R, le calcul du flux est beaucoup plus  compliqué ; il vaut mieux utiliser l'autre méthode signalée dans mon premier message...
Remarque : pour vraiment t'aider, il faudrait connaître exactement le but de cette recherche. Pour l'instant, cela ressemble un peu à des résultats de cours que tu vas démontrer plus tard dans l'année...
La courbe orientée passant par M ayant vaguement l'allure d'une portion d'ellipse est une ligne de champ...

Merci beaucoup.

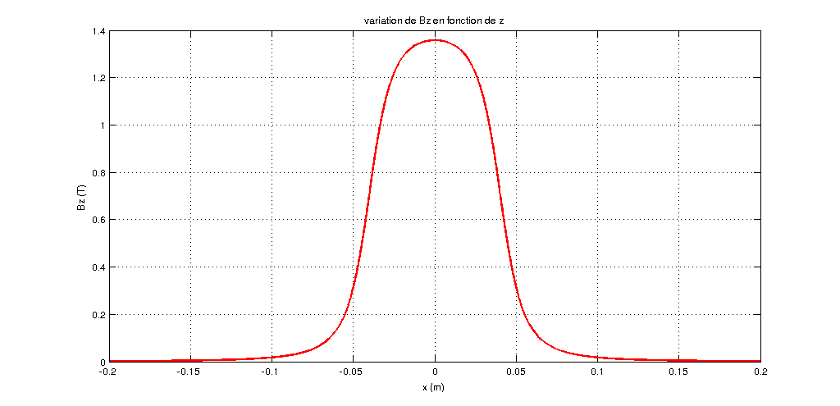
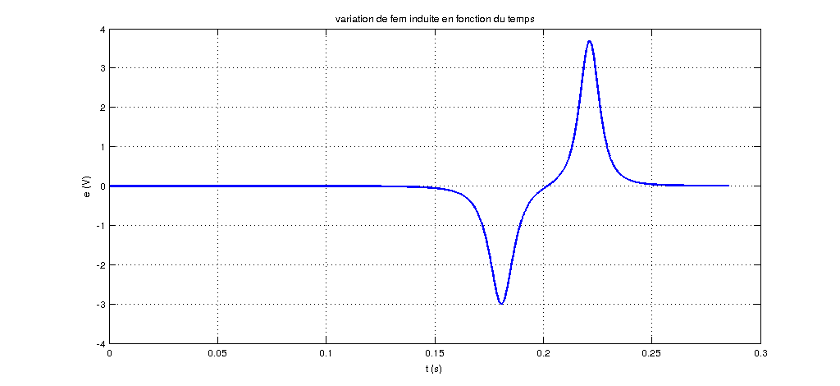
Si cela peut t'aider un peu : voici deux courbes : la première représente les variations de Bz en fonction de z avec les notations de mon message précédent. La seconde représente les variations de la f.é.m. induite à travers la bobine plate fixe quand on laisse tomber en chute libre l'aimant droit à travers, pôle nord vers le haut. Je te laisse interpréter l'allure de la courbe. Celle-ci peut être obtenue expérimentalement en reliant les bornes de la bobine plate à l'entrée d'un oscillo numérique ou à l'entrée d'une carte d'acquisition.
Autre expérience possible si tu disposes de capteur de vitesse.
Mesurer la vitesse de l'aimant après traversée, la bobine étant en circuit ouvert puis mesurer la vitesse de l'aimant après traversée les deux bornes de la bobine étant reliées par un fil de résistance négligeable. Si la hauteur de chute est la même et la position initiale de l'aimant par rapport à la bobine identique, la diminution d'énergie cinétique de l'aimant dans le second cas te donnera l'énergie totale produite par induction lors de la traversée.
Autres expériences assez simples et assez spectaculaire si tu disposes de tubes métalliques de mêmes longueurs et mêmes diamètres intérieurs et extérieurs mais constitués de métaux différents : aluminium, cuivre, plomb... (pas de fer ou acier !). On peut assez facilement montrer que la vitesse de chute d'un aimant dans un tube est constante passés les quelques premiers centimètres de chute et que cette vitesse est d'autant plus faible que le métal est bon conducteur électrique. Tu as là une méthode précise de comparaison des conductivités des métaux non ferromagnétiques...
Je ne peux guère t'en dire plus sans mieux connaître les objectifs de ton étude.

Merci pour cette réponse.

Pouvez-vous me démontrer que Bz en M garde la même valeur qu'en Mo tant que la distance de M à Mo ne dépasse pas R?

Merci

Il faut faire un développement limité de Bz en fonction de r en utilisant le fait que le rotationnel de B est le vecteur nul en Mo.
Par ailleurs il ne faut pas perdre de vue que la principale application de l'induction en rapport avec l'énergie est l'alternateur  mais je ne vois pas trop un tipe la dessus...le freinage par induction peut-être...

Merci pour tout