Bonjour,
Je vous poste ce "topic" : cet  exercice, afin que vous puissiez m'aider à éclaircir certaines informations.

Voici ci-dessous l'énoncé de l'exercice :

- Nous considérons un paquet de protéines de tailles L qui migrent dans un gel. Ce paquet a une masse M et parcourt une distance x (voir schéma en bas).
- Nous considérons un autre paquet de protéines de taille L - dL qui migrent dans le gel. Ce paquet a une masse M - dM et parcourt une distance x+dx étant donné le principe de fonctionnement du gel (voir même schéma).
- Nous faisons la supposition raisonnable que la distance parcourue dx supplémentaire est proportionnelle à dM mais inversement proportionnelle à la masse M du paquet puisque les protéines les plus longues parcourent une distance plus faible. Nous posons donc : dx = ( / M) * dM où est une constante qui dépend de la nature du gel.

1) La distance parcourue par le paquet de protéine est une fonction de sa masse et nous posons x = f(M).
Montrer, à l'aide d'un développement de Taylor au premier ordre, que la distance supplémentaire parcourue par le paquet de masse M - dM vaut : dx = - (df/dM) * dM.
2) Montrer alors que la distance parcourue a pour expression : x = -ln M + C, C est une constante (ça je le vois un peu près).

Répondez-moi quand vous aurez du temps libre (surtout pour la première question).
Je vous en serez très reconnaissant.

Merci de votre compréhension.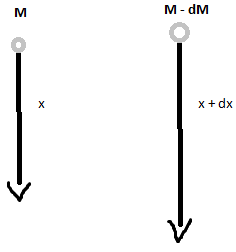



***Image recadrée***