Niveau maths sup

Projection du poids ?

Posté par
alsyia 24-08-13 à 12:23

Coucou, c'est encore moi et mes soucis de projection !

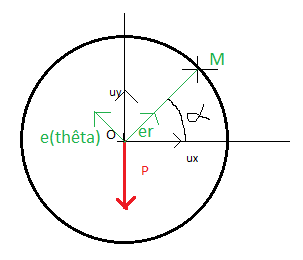
Pour la projection du poids dans la base polaire sur le schéma ci-joint, j'obtiens $\vec{P} = -mg(sin(\theta).\vec{er} + cos(\theta).\vec{e\theta})$

Pouvez simplement me confirmer que c'est la bonne réponse ? Dès que y a un angle obtus, je perds tous mes moyens...
Généralement, j'essaie de vérifier en regardant rapidement le signe des sin/cos et si ça correspond avec les sens des composantes par rapport aux vecteurs de bases. (si vous avez compris cette phrase, bravo)
Existe-il une autre méthode ?

Merci d'avance.

Projection du poids ?

Posté par re : Projection du poids ? 24-08-13 à 12:24

Oups, il faut lire alpha au lieu de thêta, désolé.

Posté par re : Projection du poids ? 24-08-13 à 12:36

Bonjour,

Les signes sont bons, si on fait $\alpha = 0$ ou $\alpha=\frac{\pi}{2}$ , c'est bon aussi.
Pour moi, c'est OK.

Posté par re : Projection du poids ? 24-08-13 à 14:59

Je n'ai pas saisi l'histoire du aplha = Pi/2, mais si tu trouve les même signes, c'est super.

Merci beaucoup !

Posté par re : Projection du poids ? 24-08-13 à 21:08

C'et important pour vérifier, le coup du $\alpha=\frac{\pi}{2}$ .

Si $\alpha=\frac{\pi}{2}$ , $\vec{e}_r$ est vertical vers le haut, $\vec{e}_\theta$ horizontal vers la gauche, et on a bien $\vec{P} = -P \vec{e}_r$ à la fois avec le dessin, et avec vos formules.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Projection du poids ?

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique