Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau autre
Partager :

Problème sur les moments des forces, expression littérale

Posté par
lapitch 12-02-13 à 12:48

Bonjour à tous,

je suis nouvelle sur ce forum et j'ai vraiment un problème sur la fin d'un exercice...Veuillez trouver cet exercice ici

** lien vers l'énoncé effacé **

C'est en fait le 4.1, le 4.2 et le 4.3 de la partie III MECANIQUE qui me posent problème...pouvez vous m'aider s'il vous plait? Je n'ai pas le cours adapté alors ce serait vraiment sympa de votre part de m'aider... J'attends un max de reponses!!

Merci beaucoup par avance!!


Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum     

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 12-02-13 à 20:20

Bonsoir,
Qu'as-tu répondu à la question 3 ?

Posté par
lapitchre : Problème sur les moments des forces, expression littérale 14-02-13 à 15:49

Bonjour,

pour la question 3 j'ai la force R qui a comme point d'application A, la droite d'action verticale partant de A et qui se dirige vers le haut d'une valeur de 1326,2N enfin je ne sais pas si je dois laisser le "-" avant pour montrer qu'elle est de sens opposé aux autres forces. Voilà. Je te remercie par avance pour ton aide...

Estelle

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 15-02-13 à 12:43

OK...
Pour savoir comment cadrer ma réponse, je suis obligé de te demander si tu connais le produit vectoriel. La vraie définition du moment d'une force utilise le produit vectoriel.
Pour les forces, il faut calculer le moment des forces. La somme des moments est nulle à l'équilibre.
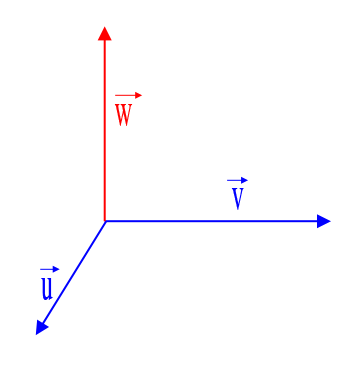
Les forces se répartissent comme sur le schéma :
d'un côté
- contrepoids
- partie AC de la planche
et de l'autre
- enfant
- partie AC de la planche
Pour le poids d'une partie de la planche, celle-ci étant homogène, la force s'applique au milieu de la partie considérée.

Problème sur les moments des forces, expression littérale

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 15-02-13 à 12:45

Petite erreur...

Citation :
d'un côté
- contrepoids
- partie AC de la planche

partie AC de la planche ==> partie AB de la planche

Posté par
lapitchre : Problème sur les moments des forces, expression littérale 15-02-13 à 13:46

Ok pour l'instant je suis...j'avoue que le produit vectoriel me dit qqchose seulement dans mon cours on en parle pas...quel est le rapport entre le produit vectoriel et les questions 4.1 4.2 4.3?Merci encore pour ton aide.

Estelle

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 15-02-13 à 16:02

Le produit vectoriel de deux vecteurs \vec{u} et \vec{v} est un vecteur \vec{w} (contrairement au produit scalaire) qui est tel que le trièdre (\vec{u},\vec{v}, \vec{w})  est direct et que ||\vec{w}||\,=\,||\vec{u}||\,||\vec{v}||\,\,sin(\vec{u},\vec{v}) .
La notation est :  \vec{w}\,=\,\vec{u}\,\wedge\,\vec{v} .
Autrement dit, le produit vectoriel est un vecteur orthogonal au plan défini par \vec{u}  et  \vec{v}   (donc orthogonal à \vec{u}  et à \vec{v}) avec la norme indiquée précédemment. Il y a aussi le sens : trièdre (\vec{u},\vec{v}, \vec{w}) direct.

Problème sur les moments des forces, expression littérale

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 15-02-13 à 16:05

Le rapport avec les questions 4.1, 4.2 et 4.3 est qu'il faut calculer les moments des forces.
Le moment d'une force \vec{F}, appliquée en un point M,  par rapport à un point O est :
\vec{M}_{\vec{F}/0}\,=\,\vec{OM}\,\wedge\,\vec{F}

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 15-02-13 à 16:22

Par exemple, le moment de la force due à l'enfant est :
\vec{M}_E\,=\,||\vec{AC}||\,\,||\vec{E}||\,\,sin(\vec{AC},\vec{E})
\vec{M}_E\,=\,(6,20\,-\,x)\,\,(20,5\,\times 9,81)\,\,sin(120°)
\vec{M}_E  est perpendiculaire au plan de la feuille et dirigé vers l'arrière :  \vec{M}_E\,=\,\vec{AC}\,\wedge\,\vec{E}\,\Rightarrow\,trièdre\,\,(\vec{AC},\vec{E},\vec{M}_E)\,\,direct

d'accord ?

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 15-02-13 à 16:50

Pour répondre plus précisément à la question 4.1, il faudrait écrire :
\vec{M}_E\,=\,||\vec{AC}||\,\,||\vec{E}||\,\,sin(\vec{AC},\vec{E})
\vec{M}_E\,=\,(L\,-\,x)\,\,(m_1\,g)\,\,sin(\alpha\,+\,\frac{\pi}{2})

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 16-02-13 à 13:17

On peut aussi voir le moment d'une force d'une autre façon...Peut-être plus simple ?...
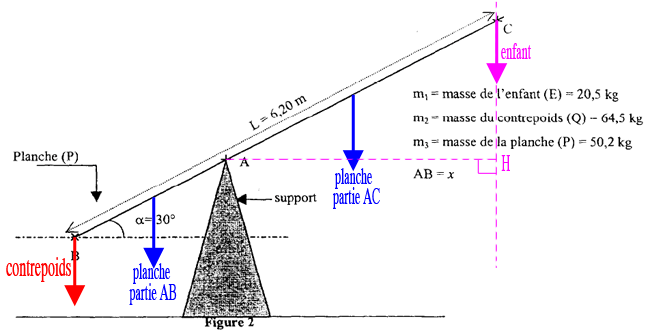
Par exemple, le moment de la force  \vec{E}  (enfant) est égal au produit de la norme de  \vec{E} par la distance AH, AH étant la perpendiculaire abaissé de A sur la direction de     \vec{E}  (autrement AH est la distance de A à la droite support du vecteur   \vec{E} )
Donc :
\vec{M}_E\,=\,E\,.\,AH
\vec{M}_E\,=\,m_1\,g\,\,(L\,-\,x)\,\,cos(\alpha)
On trouve la même valeur que précédemment puisque  cos(\alpha)\,=\,sin(\alpha\,+\,\frac{\pi}{2})

Problème sur les moments des forces, expression littérale

Posté par
lapitchre : Problème sur les moments des forces, expression littérale 18-02-13 à 12:16

Alors je comprends à peu près mais ce que j'ai du mal à comprendre c'est pourquoi est ce qu'on a le droit de "comparer" on va dire produit vectoriel et moment. Est ce que ça marche dans tous les cas? quelles sont les conditions pour utiliser le produit vectoriel? et autre chose (pour l'instant )quel est ce ce signe, ce petit triangle pas fermé?

Merci!!


Lapitch

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 18-02-13 à 15:50

Citation :
pourquoi est ce qu'on a le droit de "comparer" on va dire produit vectoriel et moment

Parce que, comme je l'ai dit dans le message "posté le 15-02-13 à 16:05", par définition, le moment d'une force est un produit vectoriel.
Citation :
Est ce que ça marche dans tous les cas?

Oui
Citation :
quelles sont les conditions pour utiliser le produit vectoriel?

Quand on a deux vecteurs, on peut toujours faire un produit vectoriel (qui est nul si les vecteurs sont colinéaires).
Citation :
quel est ce ce signe, ce petit triangle pas fermé?

C'est justement le symbole du produit vectoriel.
Il s'écrit \wedge en LaTeX ==>  \wedge
Les anglo-saxons n'utilisent pas ce symbole.
Lorsqu'on ne connaît pas ou ne maîtrise pas bien le produit vectoriel, il vaut mieux utiliser la version "bricolée" décrite dans le message "posté le 16-02-13 à 13:17" .

Comment veux-tu procéder ? Préfères-tu chercher la solution toi-même à partir des éléments que j'ai donnés ou préfères-tu que je te donne la solution que tu pourras étudier (et poser des questions ensuite ) ?

Posté par
lapitchre : Problème sur les moments des forces, expression littérale 18-02-13 à 23:18

Je préfèrerais que tu me donnes les solutions afin que décortique ta méthode quitte à le refaire ensuite toute seule. Je pense que je comprendrai mieux ainsi si ça ne te dérange pas...d'ores et déjà un grand merci pour tes explications!

Lapitch

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 19-02-13 à 11:23

OK... Je te fais ça...

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 19-02-13 à 12:09

Selon ce qui a été écrit précédemment (message posté le 16-02-13 à 13:17)
Moment du poids de l'enfant:
M_E\,=\,E\,.\,AH
M_E\,=\,m_1\,g\,\,(L\,-\,x)\,\,cos\,\alpha
Moment du poids de la partie AC de la planche :
Ce moment est équivalent au moment d'une force égale au poids de la partie AC appliquée au milieu de la partie AC.
Le poids de la partie AC est :  \large P_{AC}\,=\,m_3\,\frac{L-x}{L}\,g   (la planche étant homogène)

\large M_{AC}\,=\,P_{AC}\,.\,AC'

\large M_{AC}\,=\,P_{AC}\,\,\frac{L-x}{2}\,cos\,\alpha

\large M_{AC}\,=\,m_3\,\frac{L-x}{L}\,g\,\,\frac{L-x}{2}\,cos\,\alpha

La somme des moments à droite est donc :
\large M_D\,=\,M_E\,+\,M_{AC}\,=\,E\,.\,AH\,+\,P_{AC}\,.\,AC'

\large \boxed{M_D\,=\,m_1\,g\,\,(L\,-\,x)\,\,cos\,\alpha\,+\,m_3\,\frac{L-x}{L}\,g\,\,\frac{L-x}{2}\,cos\,\alpha}

Voilà pour le moment total à droite...

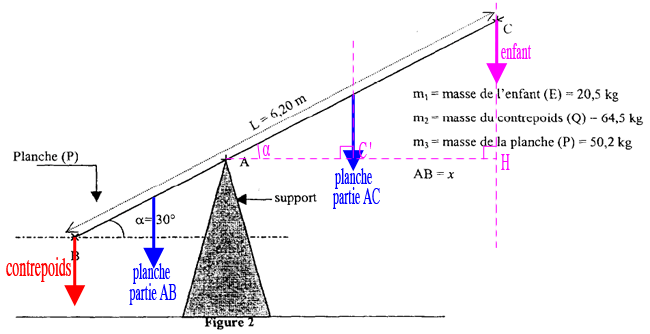
Problème sur les moments des forces, expression littérale

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 19-02-13 à 12:37

Pour les moments à gauche...
Moment du contrepoids :
\large M_Q\,=\,Q\,.\,AB'

\large M_Q\,=\,m_2\,\,g\,\,x\,\,cos\,\alpha

Moment de la partie AB de la planche :
Poids de la partie AB :  \large P_{AB}\,=\,m_3\,\frac{x}{L}\,g

Ce moment est équivalent au moment d'une force égale au poids de la partie AB appliquée au milieu de la partie AB (je peux le démontrer si tu veux).
\large M_{AB}\,=\,P_{AB}\,.\,AH'

\large M_{AB}\,=\,m_3\,\frac{x}{L}\,g\,\,\frac{x}{2}\,cos\,\alpha

La somme des moments à gauche est :
\large M_G\,=\,M_Q\,+\,M_{AB}

\large \boxed{M_G\,=\,m_2\,\,g\,\,x\,\,cos\,\alpha\,+\,m_3\,\frac{x}{L}\,g\,\,\frac{x}{2}\,cos\,\alpha}

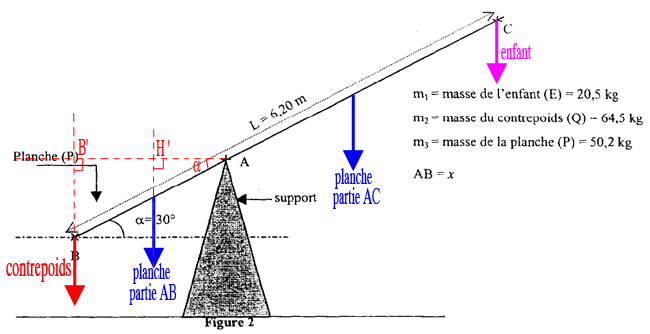
Problème sur les moments des forces, expression littérale

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 19-02-13 à 13:59

Pour "coller" un peu plus à l'exercice...
4. On se propose de calculer la distance AB notée x.
4.1 Exprimer de façon littérale les moments des forces par rapport au point A. Les distances des vecteurs-poids représentés pourront être exprimées en fonction de L, x, .
Les réponses sont :

\large M_E\,=\,m_1\,g\,\,(L\,-\,x)\,\,cos\,\alpha

\large \large M_{AC}\,=\,m_3\,\frac{L-x}{L}\,g\,\,\frac{L-x}{2}\,cos\,\alpha

\large \large M_Q\,=\,m_2\,\,g\,\,x\,\,cos\,\alpha

\large \large M_{AB}\,=\,m_3\,\frac{x}{L}\,g\,\,\frac{x}{2}\,cos\,\alpha

avec les calculs associés donnés précédemment.

4.2 Ecrire le théorème des moments au point A ; en déduire l'expression littérale de x

A l'équilibre, la somme des moments est nulle ==>  \large M_D\,+\,M_G\,=\,0

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 19-02-13 à 14:04

A suivre....

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 19-02-13 à 16:06

Donc :
Les réponses sont :

\large m_1\,g\,\,(L\,-\,x)\,\,cos\,\alpha\,+\,m_3\,\frac{L-x}{L}\,g\,\,\frac{L-x}{2}\,cos\,\alpha\,=\,m_2\,\,g\,\,x\,\,cos\,\alpha\,+\,m_3\,\frac{x}{L}\,g\,\,\frac{x}{2}\,cos\,\alpha

En simplifiant par  g\,cos\,\alpha  :

\large m_1\,\,(L\,-\,x)\,\,+\,m_3\,\frac{(L-x)^2}{2L}\,=\,m_2\,\,\,x\,\,+\,\frac{m_3}{2L}\,x^2

\large m_1\,L\,-\,m_1\,x\,+\,\frac{m_3}{2}\,L\,+\,\frac{m_3}{2L}x^2\,-\,m_3\,x\,=\,m_2\,x\,+\,\frac{m_3}{2L}x^2

Après quelques calculs :

\Large \boxed{x\,=\,L\,\frac{m_1\,+\,\frac{m_3}{2}}{m_1\,+\,m_2\,+\,m_3}}

C'est la réponse à :  en déduire l'expression littérale de x .

Pour la 4.3 (application numérique) : \large x\,=\,2,09\,\,m

Tout est à vérifier, bien entendu...

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 19-02-13 à 16:07

Dans le dernier message, "Les réponses sont :" est en trop  (c'est dû à un copier-coller mal fait ! )

Posté par
lapitchre : Problème sur les moments des forces, expression littérale 20-02-13 à 14:25

Merci pour ces explications. Je n'ai regardé qu'en diagonale pour l'instant car j'ai beaucoup de travail dans d'autres matières donc je n'ai pas encore eu le temps d'étudier ta réponse. Je reviens vers toi ce soir ou demain pour te dire comment j'ai compris et peut être pour d'autres questions...merci en tous cas!

Posté par
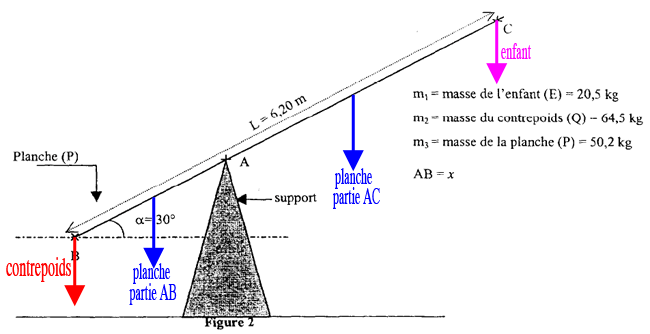
Aragornre : Problème sur les moments des forces, expression littérale 20-02-13 à 18:08

Je vais démontrer, pour compléter, le fait que le moment dû au poids P de la planche est équivalent à une force égale au poids de la planche appliquée au milieu de la planche.
Il s'agit d'une planche homogène de longueur L avec un axe en A.
On prend une "tranche" infinitésimale de la planche de longueur dr et située à une distance r de A.
On calcule le moment dM dû à cette "tranche" :
\large dM\,=\,dP\,.\,r\,cos\,\alpha

On a :
\rho : masse volumique de la planche
S    : section de la planche
La masse de cette "tranche" est donc : dm\,=\,\rho\,dV\,=\,\rho\,S\,dr
Le poids dP est donc : dP\,=\,g\,dm\,=\,\rho\,S\,g\,dr
D'où le moment élémentaire :
\large dM\,=\,dP\,.\,r\,cos\,\alpha\,=\,\rho\,S\,g\,cos\,\alpha\,\,r\,dr
Il ne reste plus qu'à intégrer de 0 à L :
M\,=\,\rho\,S\,g\,cos\,\alpha\,\int_0^L\,r\,dr
M\,=\,\rho\,S\,g\,cos\,\alpha\,\left[\frac{r^2}{2}\right]_0^L
M\,=\,\rho\,S\,g\,cos\,\alpha\,\frac{L^2}{2}
M\,=\,\rho\,S\,L\,g\,cos\,\alpha\,\frac{L}{2}
Or : m_{planche}\,=\,\rho\,S\,L
M\,=\,m_{planche}\,g\,cos\,\alpha\,\frac{L}{2}
M\,=\,P\,\frac{L}{2}\,cos\,\alpha
Donc tout se passe comme si, à la place de la planche, on avait une force égale au poids de la planche appliquée à une distance  \frac{L}{2}  c'est-à-dire au milieu de la planche.
Cette démonstration ne fait pas forcément partie de l'exercice... (c'est pour ta culture ! )

Problème sur les moments des forces, expression littérale

Posté par
Aragornre : Problème sur les moments des forces, expression littérale 22-02-13 à 15:26

Pour être parfaitement exact, dans le message "posté le 19-02-13 à 13:59" :

Citation :
A l'équilibre, la somme des moments est nulle ==>  \large M_D\,+\,M_G\,=\,0

Cette relation est exacte pour des vecteurs.
Avec la méthode que j'ai utilisée, il faut l'écrire :
\large M_D\,=\,M_G


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !