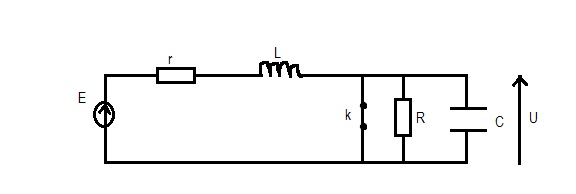
Bonsoir Lolilol,

voici une piste pour repondre a la question 1 : on appelle i(t) le courant sortant du gene de tension, et donc traversant r et L ; i1 le courant qui descend dans R ; i2, celui qui passe par C. Appelons aussi A et B les bornes communes a R et a C (conc VA - VB = u). Tu peux facilement exprinmer i, i1 et i2 en fonction de u. En ecrivant i = i1 + i2, tu obtiendras donc l'equation differentielle sur u(t).
Je connais plusieurs definitions de la "forme canonique" (tout le monde ne prend pas la meme, et bien sur chacun tient a la sienne...). D'apres la valeur de que tu donnes, je suppose que tu dois mettre l'equation differentielle precedente sous la forme d²u/dt² + 2.(du/dt) + ₀²u = 0.

Commence par faire ca, on regardera les conditions initiales apres.

Prbebo.

pour le courant i2, il passe par C mais il descend ou il monte? :s

Eh bien, les deux... puisqu'il va osciller dans le temps (on verra a la question 3 que le discriminant de l'equation caracteristique est negatif). Le courant i2 est nul avant l'ouverture de l'interrupteur (puisque les points A et B sont relies par un court-circuit), et il va redevenir nul apres un temps suffisamment long (car la capacite se sera completement chargee). Donc il sera tantot >0, tantot <0. Il en est de meme pour les courant i et i1. mais ce n'est pas grave ! Mets le circuit en equation en partant d'une situation reelle : i(t) sort du gene de tension, i1 et i2 descendent respectivement dans R et dans C. On travaille avec des courants algebriques, donc il est inutile ici de se demander quel est leur sens.

Bon, moi je suis en train de terminer la question 3...  A tout a l'heure,  prbebo.

D'accord merci beaucoup. Je vais considérer alors que i1 et i2 descendent.

Alors Lolilol, tu n'as rien trouve ?
Voici le debut du corrige :
u = vA - vB = E - ri - Ldi/dt (1), dans la branche contenant E, r et L ;
u = R.i1 soit i1 = u/R (2) dans la branche contenant r.
i2 = dq/dt = Cdu/dt (3) dans celle qui contient C.
Et enfin i = i1 + i2 (4), loi des noeuds.

On en tire avec (4) i = u/R + C.du/dt (4'), soit di/dt = 1/R.du/dt + C.(d²u/dt²) (5).
En reportant (4') et (5) dans (1), on obtient une relation dans laquelle ne figurent que u, sa derivee premiere du/dt et sa derivee seconde d²u/dt² :
LC.d²u/dt² + (rC + L/R).du/dt + (1 + r/R).u = E, qui peut s'ecrire
d²u/dt² + [(rC + L/R)/LC].du/dt + (1 + r/R)/LC.u = E/LC, soit d²u/dt² + 2.du/dt + ²u = E/LC, ou et ont exactement les expressions indiquees dans l'enonce.

Voila faite la premiere question, je t'attends pour les suivantes.  Prbebo.

Justement je bloquais pour la première question, j'arrivais pas à retrouver le 2 et le ₀² . Merci pour la première question J'essaie de faire les autres.

Désolé de te poser tant de questions :/ mais pour la question 2, pour trouver par exemple U(t=0)=0, on doit d'abord trouver l'expression de U(t) non avec les 3 étapes? Solution homogène, particulière et finale?

Pour l'expression de U(t) je trouve :

U(t) = Ae^-tcos(wt+)+E .

U(t) est continue donc U(t=0) = E = Ae⁰cos(0+)

Oups j'ai appuyé sur POSTER sans faire exprès. :/

Je suis sur la bonne voie? :/

Non, au contraire ! puisque c'est la relation u(t = 0) = 0 qui permet de trouver les constantes arbitraires A et B qu'on rencontre en integrant l'equation differentielle.

La valeur de u(t) et sa derivee du/dt a l'instant t = 0 s'obtient en appliquant les regles de continuite, que tu as forcement vues dans ton cours et qui s'exposent ainsi :
a)  pour un condensateur, la charge q portee sur les plaques et donc la difference de potentiel v = q/C a ses bornes ne peut presenter de discontinuite. En effet si c'etait le cas, la derivee dq/dt ( ou dv/dt) serait infinie et le courant qui le traverse, i = dq/dt = C.dv/dt le serait aussi : impossible physiquement. Ceci revient a dire que si on envisage un instant t₀ quelconque, ainsi que les instants t₀^- et t₀⁺ justes avant et apres cet instant t₀, q(t₀^-) = q(t₀⁺) et v(t₀^-) = v(t₀⁺). Pour parler plus simplement, on doit pouvoir dessiner les fonctions q(t) et v(t) sans lever le crayon.
b)  idem pour un circuit qui contient une inductance parcourue par un courant i(t) : i(t₀^-) = i(t₀⁺), sinon la tension Ldi/dt deviendrait infinie.
Si on applique ces deux regles a l'instant initial :
a)  pour u(t) : avant l'instant initial u(0^-) est nul (condensateur non charge). Donc u(0⁺) est nul, ce qui donne u(t = 0) = 0.
b)  pour le courant i(t) : avant l'instant initial i(0^-) = E/r (tout le courant qui sort du gene de tension passe par le court-circuit constitue par l'interrupteur ferme). Donc i(0⁺) = E/r egalement. Or on a vu que i(t) = u/R + C.du/dt, donc a l'instant initial, sachant que u(0) = 0, on en tire E/r = 0 + C.(du/dt)(t=0), ce qui donne la valeur de la derivee de u(t) a cet instant : du/dt pour t = 0 = E/rC.
Ca y est, lorsque tu auras integre l'equation differentielle donnant u(t), tu l'obtiendras en fonction de deux constantes arbitraires A et B, dont l'expression pourra etre obtenue grace aux deux conditions initiales portant sur u(0) et sa derivee a cet instant.

OK ? sinon ecris-moi.  Prbebo.

Non Lolilol, le second membre n'est pas E, mais E/(1 + r/R)ou encore E.R/(r + R). Facile a expliquer ! Lorsque le regime limite sera etabli, le courant i sortant du generateur sera constant et le condensateur ne se  chargera plus. Ca veut dire que ce courant traversera r, puis la self mais sans provoquer de perte de potentiel (puisque di/dt nul...), puis traversera R integralement. Le circuit sera alors equivalent a une fem E en serie avec deux resistances r et R, et on cherche la tension u aux bornes de R : un pb facile si on connait larelation du diviseur de tension : u = ER/(r + R).
En d'autres termes... refais tes calculs !

Je t'avoue que j'ai un peu du mal :/
Donc à la fin j'aurais une expression en fonction de deux constantes A et B?
Et avant il faut que j'intègre l'équation différentielle donnant U(t) mais il faut la trouver cette équation différentielle ou c'est celle qu'on a trouvé dans la question 1? :/

Arf donc mon U(t) n'est pas correct. Je dois remplacer mon E par E/(1 + r/R) ?

Bonjour Lolilol,

desole, je soir je coupe mon ordi a 23 heures... sinon je pourrais passer toute la nuit sur le forum !
Oui, la limite prise par u(t) est bien E/(1 + r/R) ; je t'en ai donne une explication physique hier en etudiant l'etat du circuit lorsque t -> l'infini : i(t) devient constant, donc la self ne est equivalent a un fil sans resistance et i(t) passe integralement dans R2 et non plus dans C, d'ou le diviseur de tension (r, R).
Aujourd'hui je vais te donner une autre pruve, en s'appuyant sur l'equation differentielle que j'ai etablie hier :
Lorsque le regime transitoire a disparu, u(t0 (comme i, i1 et i2) tendent vers des constantes, ceci parce que la source d'alimentation est une fem E constante). Ca veut dire que du/dt et d²u/dt² sont nuls. Si tu reportes ces deux derivees dans l'equa diff, tu obtiens 0 + 0 + ²u = E/LC, ce qui donne u = E/(LC²). Et si tu remplaces ² par l'expression qui t'estt donnee dans l'enonce, et que j'ai retrouvee, tu obtiens u = E/(1 + r/R). L'equation differentielle contient donc bien, non seulement l'evolution temporelle de u(t) lorsque le regime transitoire est installe, mais aussi la solution limite prise pas u lorsque le transitoire n'est plus la, et ca c'est tres important. Il ne restera plus qu'a regler les valeurs des constantes A et B en fonction des conditions initiales pour avoir la solution complete depuis t = 0 jusque t infini.

Pour ta remarque "Je t'avoue que j'ai un peu du mal :/ " : ne te decourage pas c'est normal, on y est tous passes et au bout d'un moment ca devient simple !

Prbebo.

D'accord merci de me consacrer du temps pour m'expliquer . Oui ça viendra avec de l'entrainement!
Mais ce que je me pose comme question, c'est comment on trouve les constantes A et B? On devrait avoir une expression de U(t) avec A et B non? et faire U(t=0) = 0 ?

C'est parce que tu n'a pas encore bien compris le processus :
a)  la solution de l'equation differentielle est u(t) = e^-t.(Acost + Bsint) + E/(1 + r/R). (Rappel : c'est la somme de la solution de l'equation sans second membre, appelee equation honogene, et de la solution particuliere de l'equation avec ce second membre, qui est E/(1 + r/R) et que je t'ai justifiee 2 fois).

b)  A ce stade tu as trouve u(t) mais avec deux parametres a trouver, les constantes d'integration A et B. Cad que mathematiquement, quelles que soient les valeurs de A et de B, si tu reportes cette expression de u dans l'equation differentielle celle-ci sera toujours satisfaite : elle possede donc une infinite de solutions. En physique, un probleme qui a une infinite de solutions ca n'existe pas. Donc A et B ont forcement une valeur unique. On trouve ces deux valeurs en se placant au debut du regime transitoire, cad a t = 0. C'est l'objet de la question 2 dont je t'ai donne les reponses dans mon post d'hier 22h40 : a t = 0, u est nul et sa derivee du/dt vaut E/rC. Ceci donne deux equations dont les inconnues sont A et B. On peut donc arriver a trouver ces deux constantes.

A titre d'exemple : si je fais t = 0 dans l'expression de u(t), j'obtiens u(0) = A + E/(1 + r/R) = 0, ce qui donne A = -E/(1 + r/R). Pour l'autre relatin tu dois calculer la derivee du/dt (non, ce n'est pas difficile !), puis y faire t = 0 et egaler le resultat avec E/rC. Ca te donnera B.

A toi, je vais faire une course (ce soir c'est Hallowen dans le quartier et je n'ai plus de bonbons...). Je reprends l'antenne vers 18 heures.

BB.

Re prbebo,

J'ai fais ce que tu m'as dis, j'ai dérivé U(t), alors ça m'a donné :

Sachant que la dérivée de E/(1+(r/R)) = 0,

du/dt = -e^-t(Acost+Bsint)+e^-t(-Asin(t)+Bcos(t))

car (uv)' = u'v+uv'

Désolé j'avais pas terminé j'ai posté sans faire expres. :/

donc pour du/dt(t=0)= A + B = E/rC

B = (E/rC)- A B = [(E/rC)-A]/ !

Est-ce correct?

Je ne suis pas sure de la dérivée.

Désolé je me suis trompé dans les calculs.

J'ai oublié le - ^^' !

donc ça nous donne :

-A+B = E/rC

B = [(E/rC)+A]/

C'est correct maintenant?

Je ne répondrais plus après 20h car je ne suis pas chez moi ce soir. (Halloween ^^' )
Je te préviens au cas où tu attendrais une réponse toute la soirée lol
Je serais de retour demain.

Desole de t'avoir fait attendre...

Pour la derivee de u(t) tu as trouve du permier coup. Ensuite, en effet pout t = 0 elle vaut -A + B. Comme cette derivee vaut E/rC et que A vaut -E/(1 + r/R) trouve avec u(0) = 0, on obtient B = (E/).[1/rC - /(1 + r/R)].

Bon, on commence a voir le bout de cet exercice mais je te rappelle que tu n'as pas repondu a la question 3 (calculer numeriquement et pour constater que le discriminant est negatif), ni a la question 4 (calculer numeriquement les constantes A et B et tracer le graphe de u(t).

On voit ca demain ?  Prbebo.

Pas de soucis .
A demain!

S'agissant de la question 3, je n'ai pas trop compris par contre ce qu'il fallait faire du ² = ₀²-², du moins je ne sais pas comment m'en servir pour trouver U(t) en fonction de , et des données initiales.

Faut-il que j'injecte U(t), càd, e^-t(Acost+B.... dans l'équadiff?

Bonjour Lolilol,

pour la question 3 j'ai simplement calcule et ₀ en appliquant les relations donnees dans l'enonce (et retrouvees dans mon post du 30/10 a 21h30) : j'obtiens = 55 s^-1 (une etude d'homogeneite montre facilement que , comme ₀, se mesure en s^-1) et ₀² = 1.001 s^-2, soit ₀ = 1000.5 s^-1. dans ces conditions il n'y a pas photo : le discriminant reduit ' de l'equation differentielle d²u/dt² + 2.du/dt + ₀²u = 0 (a ce propos, je viens de me rendre compte qu'il y a une petite faute de frappe dans om post du 30/10 21h30 : j'ai ecrit au lieu de ₀... desole) est ' = ² - ₀², nettement negatif. On pose donc ' = i.(-') = i(₀² - ²) = i. Les racines de l'equation caracteristique sontalors r₁ = - - i et r₂ = - + i, et lorsqu'on prend les exponentielles de r₁t et r₂t pour obtenir la solution de l'equation , les exp(-t) se mettent en facteur et les exp(it) finissent par donner les lignes trigonometriques cost et sint. C'est pourquoi la solution de l'equation homogene (cad sans le second membre) s'ecrit uh(t) =e(^-t)(A.cost + B.sint), a laquelle bien sur il faut ajouper la solution particuliere up = E/(1 + r/R) pour obtenir la solution complete. OK ? Tu ne peux pas appliquer la relation ² = ₀² - ² pour calculer ₀, puisque tu ne connais pas ²... en revanche l'inverse est possible, et avec les valeurs de et de ₀ ci-dessus on voit facilement que est pratiquement egal a ₀. C'est normal puisqu'on est en amortissement tres faible (l'amortissement est mesure par ), ce qui equivaut a dire qu'il y aura beaucoup d'oscillations avant que u(t) ne se stabilise a sa valeur limite. Et en te disant  ca, je te donne un sacre coup de main pour repondre a la question 4...

Je  vais maintenant couper le contact jusqu'a ce soir, car je fais du soutien scolaire a domicile a une etudiante de 1ere, la seance c'est demain matin et il est grand temps que je lui concocte une feuille d'exercices...

Continue quand meme a poster  si tu as encore des questions.

B.B.

Merci beaucoup pour le coup de main. J'essaierai de faire la question 4 moi-même. Si j'ai des questions je posterais sinon merci de m'avoir aider!