Inscription / Connexion Nouveau Sujet
Problème : Mouvement d'un anneau sur une piste circulaire
Bonjour, j'aurai une question à propos de ce petit problème.
J'ai réussi à résoudre jusqu'à la partie B/ 4. Mes résultats me semblent plutôt cohérent et c'est pas trop là le problème.
Mon problème, c'est à partir de la question 4. Naïvement, j'aurai bien envie de dire que le vitesse initial doit-être positive (vu que v = R1*teta < 0 pour teta = -pi/2) et je ne sais pas et ne vois pas pourquoi ça pourrait-être ça. D'où je pense que c'est faux ^^
Donc voilà ! Je ne sais pas du tout quoi faire pour avancer !
Et sinon, je pense que pour la 5) c'est en utilisant le théorème de l'énergie cinétique en M dans le référentiel du laboratoire et de dire que Em(F) = Em(A) (puisque l'énergie mécanique se conserve).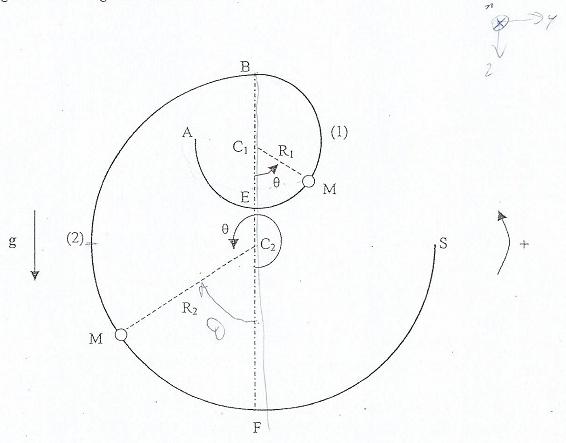
** énoncé effacé ; image laissée **
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Désolé, je ne trouve pas de bouton pour éditer mon message, j'écrirai l'énoncé la prochaine fois.
Pour l'énoncé "On considère le dispositif de la figure ci-dessus, où un anneau assimilable à une particule M de masse m se déplace solidairement à une piste fixe formée de deux parties circulairs (1) et (2) de rayon R1 et R2, de centre C1 et C2, dans un plan vertical. On supposera R2 > R1.
Partie 1) La particule est comprise pour un angle 
 [-
[- /2 ;
/2 ;  [
[
Partie 2) La particule est comprise pour un angle 
 [
[ ; 5
; 5 /2[
/2[
Dans la première partie, on souhaite :
Déterminer (d /dt)² à un instant quelconque.
/dt)² à un instant quelconque.
Puis, on émet l'hypothèse que l'amplitude des oscillations est faible, d'où sin =
=  et on souhaite déterminer
et on souhaite déterminer  (t)
(t)
Donc, j'ai utilisé le fait que l'énergie soit conservative (la réaction du support ne travaillant pas car il n'y a pas de frottement). J'en ai conclu que Em(M) = /dt))²}{2}" alt="\frac{m(R1*(d
 /dt))²}{2}" class="tex" /> - mgR1cos(
/dt))²}{2}" class="tex" /> - mgR1cos( ).
).
J'ai ensuite utilisé l'hypothèse (donné par l'énoncée) que à t=0, la particule est en E,  =0 et la vitesse angulaire est positive.
=0 et la vitesse angulaire est positive.
Ce qui m'a donné (d /dt)² = (d
/dt)² = (d /dt)0² + 2gR1(cos
/dt)0² + 2gR1(cos - 1)
- 1)
De là pour déterminer  (t), j'ai dérivée l'énergie mécanique pour obtenir l'intégrale première du mouvement :
(t), j'ai dérivée l'énergie mécanique pour obtenir l'intégrale première du mouvement :
0 = R1 (d² /dt²) + gsin(
/dt²) + gsin( ) = 0
) = 0
D'où après utilisation de l'hypothèse (sin =
=  ) et des conditions initiales, j'obtiens :
) et des conditions initiales, j'obtiens :  (t) =
(t) = /dt)0}{w0}" alt="\frac{(d
 /dt)0}{w0}" class="tex" />sin(w0t) avec w0² =
/dt)0}{w0}" class="tex" />sin(w0t) avec w0² =
Donc ça, c'était pour la première partie. Dans la seconde partie, on nous demande d'exprimer l'énergie potentiel de pesanteur en sachant que Ep = 0 pour =
= 
Désolé... J'ai eu un bug de pc...
Pour réécrire les formules qui ne sont pas passé : Em = m(R1(d /dt))²/2 - mgR1cos
/dt))²/2 - mgR1cos + C
+ C
et  = [(d
= [(d /dt)0/w0] sin(w0t)
/dt)0/w0] sin(w0t)
Donc ! Pour la deuxième partie, pour exprimer l'énergie potentiel, j'ai juste remplacé mes deux expressions (celle de la partie 1 et de la partie 2) pour définir la constante, d'où j'obtiens :
Pour la partie 1) Ep = mgR1(-1 - cos )
)
Pour la partie 2) Ep = mgR2 (-1 - cos )
)
On nous demande ensuite de tracer la fonction, et de définir les positions d'équilibres de l'anneau. Donc, c'est lorsque (d /dt) = 0, ce qui est pour
/dt) = 0, ce qui est pour  = k
= k où k est un entier naturel.
où k est un entier naturel.
Mon problème arrive à partir de ce moment ! On demande à quelle condition sur la vitesse V0 l'anneau peut-il atteindre le point F. Sur le même soucis, je ne vois pas à quelle condition sur V0 l'anneau sort-il de la piste en S.
J'ai pensé, comme dit dans mon premier message, que V0 doit-être positive. Mais je ne serai l'expliqué et ça me semble faux...
Voilà !
Encore désolé pour les multiples posts, mais je ne trouve pas de bouton pour éditer u.u
Merci d'avance pour les réponses !
Merci ^^
J'aurai juste besoin de savoir si j'ai bien compris le raisonnement.
On sait que Ec > 0 d'où Em - Ep > 0, donc pour que l'anneau arrive à la position F, il faut qu'il puisse arriver au point B. (barrière de potentiel ?)
Pourquoi l'anneau doit-il avoir une vitesse limite en B de 0 ?
Pour la suite je pense avoir compris le raisonnement, je vais essayer et voir ^^
Mais vraiment merci !



