Inscription / Connexion Nouveau Sujet
Problème masse poulie
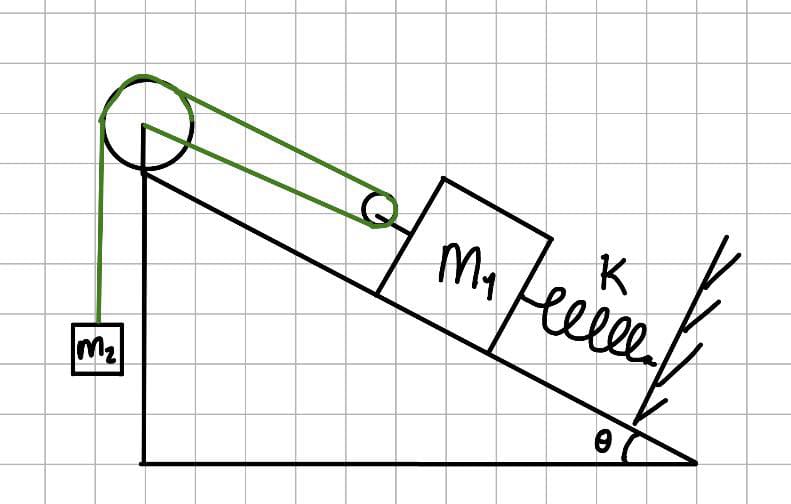
Considérant qu'il n'y a aucune friction sur le plan incliné, et que l'axe des x est parallèle au plan incliné et que l'axe des y est perpendiculaire au plan incliné, trouver la fréquence d'oscillation, soit w, autour de la position d'équilibre de ce système.
Bonjour,
Rappel de la règle 6 du forum :
merci donc de proposer vos pistes de réflexions pour résoudre votre exercice
Bonjour, honnêtement avec cet exercice je ne sais pas par ou commencer... J'ai commencé par faire le DCL de la masse M ainsi que celui de la masse m. Ensuite, je me suis dit que puisqu'on cherche la fréquence d'oscillation autour de la position d'équilibre je devait commencer part trouver cette position d'équilibre. J'ai donc trouver; x=mg-Mgsin(angle)/k qui serait ma position d'équilibre. Par la suite en observant la corde reliant les deux blocs et la manière dont celle-ci est enroulée, j'ai trouver que l'accélération des deux blocs ne semblait pas être la même puisque la masse m descend deux fois la distance que la masse M parcourt. En considérant le système d'axe choisit, j'ai donc trouvé amsin(angle) = 2aM. Cependant, à partir de là je suis complètement bloqué... Je pensais prendre la formule X " + W(exp 2) + x = 0 pour trouver la fréquence angulaire W, mais puisque l'accélération des deux blocs ne semble pas être la même je ne sais plus par quel chemin passer. Quelqu'un pourrait m'aider ? Merci beaucoup 
Bonjour,
Je ne sais pas ce qu'est le DCL.
Dans un problème de ce type, l'étape 1 c'est la cinématique : ici trouver le rapport entre le mouvement de m1 et m2 (c'est votre "par la suite").
Il n'y a aucune nécessité de trouver la position d'équilibre.
Avez-vous vu les méthodes énergétiques (dans le cas présent c'est le plus rapide) ?
Bonjour, merci pour votre réponse. Le DCL décrit un diagramme du corp libre. Oui, je crois me souvenir de la méthode énergétique.. Cependant je ne saurai pas comment l'appliquer dans ce cas-ci... Est-ce que vous voulez dire que je devrais utiliser la formule Ef = Ei? Comment vais-je être capable d'intégrer les deux accélérations dans ce problème..?
Bonjour,
Je ne connais pas non plus le " diagramme du corps libre".
Pour la méthode énergétique, je voulais dire : écrire l'expression de l'énergie du dispositif en fonction, disons, de x1. Il suffit alors d'identifier le ω2. Si cela ne vous parait pas évident, dériver l'expression, tenez compte de Ef=Ei sous la forme E=cte et vous aurez votre x"+ω^2x=0.
Remarque : que signifie "Master" ? On a l'impression d'un sujet de L1.
D'accord, mais comment pouvons nous identifier le ω2 ? Je suis désoler de vous faire répéter, mais je ne vois pas quel chemin prendre 
Si vous ne pouvez identifier ω2 directement sur l'expression de l'énergie, vous dérivez celle-ci et cela vous donnera une équation du type x"+ω^2x=0 et vous pourrez utiliser ce que vous avez vous-même proposé.
Qu'obtenez-vous pour l'énergie ?


