Inscription / Connexion Nouveau Sujet
Problème: expression quadratique de l'énergie potientielle
Bonjour,
Alors l'énoncé, on considére un pendule simple, de masse m, un fil tendu de longueur l, avec un angle thêta avec l'axe Ox orienté vers le bas tel que l'énergie potentielle totale vaut Ep= -mgx+ cste= - mgl*cos(thêta) + cste. Jusque là pas de problème, je trouve après que la positin d'équilibre est lorsque thêta = 0, puis comme thêta est très inférieur à 1 on considére que cos(thêta) équivaut à 1- ((thêta) ^2\2), c'est cela que je ne comprends pas.. Puis on arrive sur Ep équivalent à (1\2)*mgl*(théta)^2 en remplaçant, ça c'est compris.
Voilà c'est l'équivalence du cos(thêta) qui me pose problème et comment savoir à quelle moment faut utiliser les équivalences
Merci d'avance pour vos précieuses réponses
Bonjour
Il est possible que tu n'ais pas encore étudié en mathématique la notion de développement limité de Taylor. On peut démontrer que le cosinus peut s'écrire comme une somme infinie de termes :
Si , les termes en
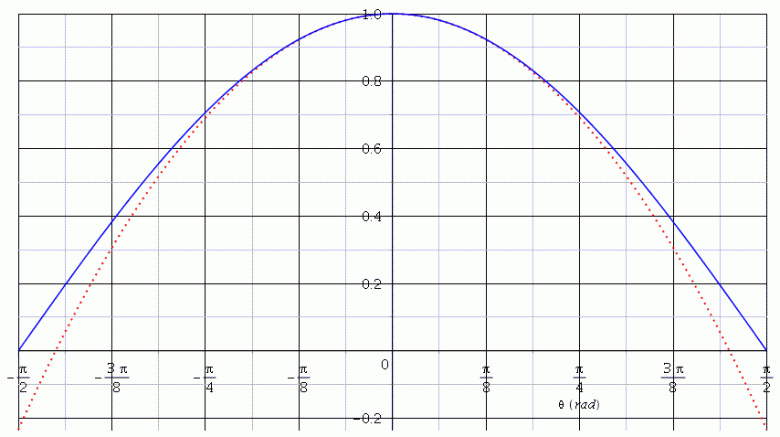
4, 6, 8, etc sont totalement négligeable devant (1-2/2), d'où l'approximation faite. Pour illustrer cela, je représente ci-dessous en bleu la courbe correspondant aux variations de cos() pour 
[-
/2 , /2] ; j'ai représenté en pointillés rouge la courbe correspondant à (1-2/2) sur le même intervalle. On voit bien que, pour une valeur absolue de inférieure à (/8)rad environ, les deux courbes sont pratiquement confondues.
Annuler
connectez vous