Inscription / Connexion Nouveau Sujet
Problème exercice mécanique solide
Bonjour, en voulant m'entraîner sur la mécanique solide je suis tombé sur un exercice sur internet pour lequel je ne trouve pas la même valeur que la correction et cette correction ne présentant que le résultat sans le détail je ne parviens pas à trouver mon erreur !
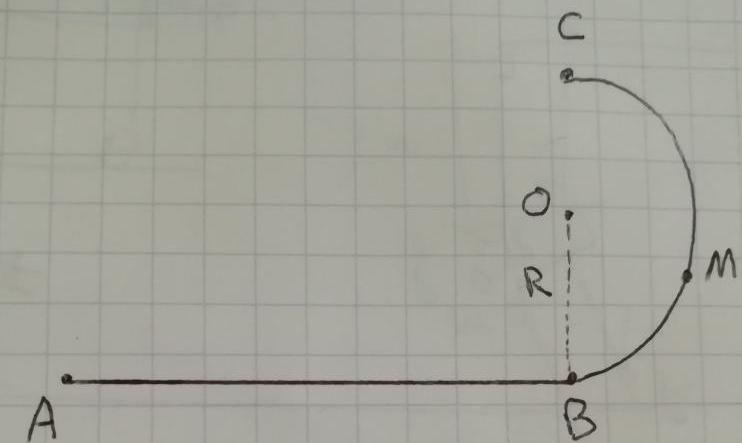
Je vous mets l'énoncé : Un solide ponctuel de masse m est lancé en A sur
une piste horizontale prolongée par un demi-cercle vertical de rayon R.
On donne : AB = 1 m ; R = 1 m ; m = 0, 5 kg ; g = 9, 81 m.s−2. Les frottements étant négligeables, calculer en A la vitesse minimale vA,min que doit avoir la masse pour qu'elle atteigne le point C.
Mon raisonnement : J'ai commencé par appliquer le théorème de conservation de l'énergie mécanique entre les points A et C. En A la hauteur est nul (zA = 0) et en C la vitesse est nul (vC = 0).
J'en suis donc arrivé à vA =  2gzC
2gzC
Je pense que jusqu'ici tout va bien et ensuite je trouve que zC = 2R et donc je trouve vAmin =  4gR
4gR
Seulement la correction (rapide !) donne  5gR
5gR
Si quelqu'un pouvait m'expliquer mon erreur ce serait top merci beaucoup !
Bonjour
Pour que le mobile reste en contact avec la piste jusqu'au point C, il faut que la force exercée par la piste sur le mobile (réaction normale Rn) reste positive tout le long de la piste. Il faut donc appliquer le théorème de l'énergie cinétique comme tu l'as fait pour obtenir VC2 mais il faut aussi appliquer la relation fondamentale de la dynamique en C et écrire : Rn 0.
0.
Bonjour vanoise, merci beaucoup pour ta réponse mais je ne suis pas sûr de bien comprendre ta réponse. Faut-il que j'applique le PFD au point C pour obtenir l'expression de Rn ? Dans ces cas là que faire de cette valeur dans mon théorème de conservation de l'énergie mécanique ? Encore merci
Salut Priam, en cours on considère que dans ce genre d'exercice la vitesse au point d'arrivé est nul. Si ce n'est pas le cas (et c'est tout à fait possible) cet exercice requiert des compétences dépassants mon niveau.
Il te faut revoir l'expression de l'accélération dans le cas d'un mouvement circulaire. Tu projettes alors l'expression vectorielle de la relation fondamentale de la dynamique sur un axe vertical. Commence par faire cela et tu verras alors l'intérêt de connaître l'expression de Vc2 que l'on déduit du théorème de l'énergie cinétique. Tu peux faire un schéma représentant les différents vecteur forces en M puis en C. Tu peux scanner ce schéma et le poster sur le forum si tu veux.
Pour avoir une accélération normale non nulle en C, il faut évidemment une vitesse non nulle en C. Si tu ne connais pas l'expression générale de l'accélération lors d'un mouvement circulaire, tu vas effectivement avoir du mal avec cet exercice !


