Bonjour,
Au niveau des deux surfaces de contact, les matériaux sont les mêmes ; il est réaliste d'imaginer que les états de surfaces sont identiques ; dans ce cas, il est réaliste de considérer les deux coefficients de frottement identiques.
Indication sous réserve : sans connaître le contexte général de cette étude et sans schéma, difficile d'être précis et rigoureux...
Tout de même, vue la symétrie apparente du problème, la limite du glissement ne peut pas être obtenue simultanément des deux côtés avec deux coefficients de frottement différents. Cela aussi : sous réserve...

Bonjour vanoise et merci pour cette réponse rapide,

Pour les coefficients de frottements, on peut très bien imaginer que les matériaux aux surfaces soient différents et donc on aurait fh différent de fb. En fait, y'a même pas besoin de se placer à la limite du glissement. Si on suppose que le pavé glisse et reste parfaitement horizontal (on aura donc Th=P*fh et Tb=P*fb et somme des moments = 0) , on aboutit à la même conclusion bizarre fh=fb. Oui désolé j'aurai peut être dû mettre un schéma pour y voir plus clair mais j'ai pas trouvé comment faire.

Toujours sous réserve...
Si tu suppose le mouvement de glissement en translation avec deux coefficients de frottement différents, la pression exercée par chaque "mâchoire" de l'étau sur la surface de contact avec le pavé ne va pas être uniforme. Conséquence : il n'est plus possible de modéliser l'action d'une mâchoire sur la surface de contact par une force appliquée au centre de la surface

J'ai du mal à comprendre pourquoi  la pression exercée sur la surface de contact avec le pavé n'est pas uniforme. Toutes les forces sont constantes non ? On a -P sur la surface en haut P sur la surface en bas (parce que le pavé ne se déplace pas verticalement), ensuite on a la force F sur O qui n'intervient pas dans le calcul des moments tout comme P et -P parce que leurs bras de levier est nul. Et du coup, d'après somme des moments=0 on a  Th=Tb. Il y a bien les 2 surfaces de contacts qui frottent donc P*fh=Th, P*fb=Tb et donc fh=fb. A moins, qu'on ne puissent pas appliquer P*fh=Th mais alors j'ai pas du tout compris pourquoi

Une piste de réflexion : supposer une répartition de pression non uniforme revient à modéliser les actions des mâchoires par des forces légèrement décalées comme indiqué sur mon schéma. Je néglige l'action du poids et me place dans l'approximation quasi statique en supposant l'existence de glissement. Les lois de la statique conduisent selon moi à :

Une différence entre les coefficients de frottement est donc tout à fait possible.
Sans être sûr que cela réponde à ta question...

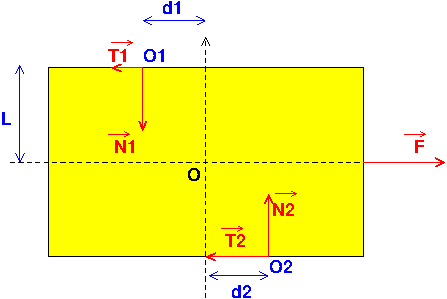
D'accord, merci d'avoir pris autant de votre temps pour me répondre. En fait, la seule chose qui ne me paraissait pas claire, c'est le fait que O1 et O2 soient forcément pas alignés (d1=d2=0). Mais en pratique, il y a forcément un décalage même s'il est infime c'est bien ça ? C'est finalement un problème assez compliqué, ça remet en cause la mécanique du point.

Bonne soirée