Bonjour, je n'arrive pas à faire cette question (je trouve F_m = -9475N ....)
pourriez vous m'aider merci

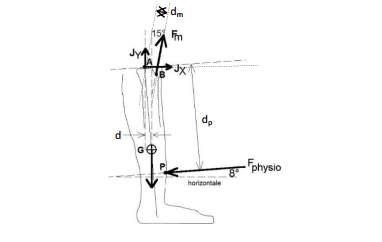
La jambe (tibia + pied) est soumise aux efforts suivants :
- Son poids : le centre de masse de la jambe est situé en G, situé à la distance d en avant
du centre de l'articulation A. La masse de la jambe est notée M.

- La force appliquée par le praticien F _physio , appliquée perpendiculairement au tibia (le tibia est d'axe AG), à un angle α=8° de l'horizontale et à une distance d_p de l'articulation. On note P le point d'application de cette force.
- La force appliquée par le muscle quadriceps F _m , en B (bras de levier d_m), inclinée de β=15° avec la verticale
- La force J appliquée par le fémur à l'articulation A. On décompose cette force en une
composante horizontale Jx et une composante verticale Jy.

1) Ecrire l'équilibre rotationnel de la jambe en A. En déduire l'expression de la force
musculaire du quadriceps F _m en fonction de tout ou partie de (M, g, F_physio, d, d_m, d_p, ,α, β), où g est l'accélération de la pesanteur

Ce que j'ai fais:
les composantes de J sont appliqués en A donc elle sont nulles pour l'équilibre rotationnel
on a (ce sont des vecteurs)
AG^Mg + AP^F_physio + AB^F_m=0
-dMg + d_p(-F_physiocos () - F_physio sin()) + d_m(F_msin() + F_mcos())

il semblerait que ça soit faux. vous pouvez m'aider? merci