Inscription / Connexion Nouveau Sujet
Probleme équilibre des moments
Bonjour, je ne comprends pas comment résoudre cette question. je suppose que le moment est: M= F L
mais je ne trouve pas de somme des forces cohérentes. Quelqu'un pour m'aider? merci 
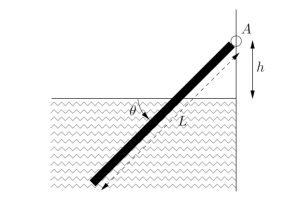
Une barre mince de longueur L, constituée par un matériau plus léger que l'eau, est
accrochée à un mur en un point A, autour duquel elle peut tourner. L'autre extrémité de la
barre plonge dans l'eau. Le point A est à une hauteur ℎ par rapport au niveau de l'eau. On
notera 𝑑 la densité du matériau.
En écrivant l'équilibre des moments, calculer l'inclinaison 𝜃 de la barre.
Salut,
Voila ce que j'aurais répondu mais je ne suis vraiment pas un expert...
 +
+ = 0
= 0
J'en viens à -L*d*9.81+1000*L/x *9.81 = 0 avec x la longueur sous l'eau.
En simplifiant x=1000/d
donc  =arcsin(h/(L-1000/d))
=arcsin(h/(L-1000/d))
Voila mon premier avis, je ne sais pas s'il y a d'autres forces... Je te conseille d'attendre la réponse de quelqu'un qui si connait plus comme Vanoise par exemple 
Bonsoir,
La tige de longueur L, de masse m, de masse volumique
où est la masse volumique de l'eau et d la densité de la tige, a une longueur hors de l'eau
et donc une longueur immergée :
. L'aire de sa section droite est S. La partie immergée est soumise à la poussée d'Archimède assimilable à une force verticale ascendante appliquée au milieu de la partie immergée c'est à dire à la distance de A :
.
L'intensité de cette force est égale au poids d'eau déplacée par la partie immergée de la tige :
Sachant que la masse de la tige est : , on obtient finalement en multipliant par L/L :
Sachant que l'action de la pesanteur est équivalente à une force mg verticale descendante appliquée à la distance L/2 du point A, le théorème des moments appliqué au point A doit conduire à la condition d'équilibre :
Je te laisse continuer. Toutes les grandeurs littérale que j'ai introduites au cours du raisonnement devraient logiquement disparaître par simplification... On obtient une expression assez simple de en fonction seulement de L, h et d.
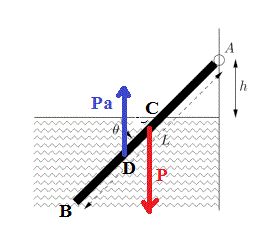
Le poids P de la barre peut être considéré comme appliqué au milieu de la barre.
Pa, la poussée d'aechimède de l'eau sur la partie immergée de la barre peut être considérée comme appliquée au miloeu de la paribe immergée de la barre (donc au milieu de [BC]).
-----
AC = h/sin(theta)
BC = L - h/sin(theta)
AD = AC + BC/2
AD = h/sin(theta) + L/2 - h/(2.sin(theta))
AD = h/(2.sin(theta)) + L/2
-----
La somme des moments des forces P et Pa autour de A est nul --->
P * AC.cos(theta) - Pa * AD.cos(theta) = 0
P * AC - Pa * AD = 0
P * h/sin(theta) - Pa * (h/(2.sin(theta)) + L/2) = 0
-----
P = k * L * d (k : coefficient réel)
Pa = k * BC * 1 (1 = densité de l'eau)
-----
k * L * d * h/sin(theta) - k * BC * 1 * (h/(2.sin(theta)) + L/2) = 0
k * L * d * h/sin(theta) - k * (L - h/sin(theta)) * 1 * (h/(2.sin(theta)) + L/2) = 0
L * d * h/sin(theta) - (L - h/sin(theta)) * (h/(2.sin(theta)) + L/2) = 0
Posons h/sin(theta) = X
L * d * X - (L - X) * (X/2 + L/2) = 0
2 * L * d * X - (L - X) * (X + L) = 0
2LdX - LX - L² + X² + LX = 0
X² + 2Ld.X - L² = 0
X = -Ld + RCarrée(L²d² + L²) (car X > 0)
h/sin(theta) = -Ld + RCarrée(L²d² + L²)
sin(theta) = h/(RCarrée(L²d² + L²) - L.d)
theta = arcsin[h/(RCarrée(L²d² + L²) - L.d)]
-----
Rien relu et donc bonne chance d'erreur. 
Attention que vanoise n'a pas utilisé le même "theta" que dans l'énoncé.


 vect + Pvect=0
vect + Pvect=0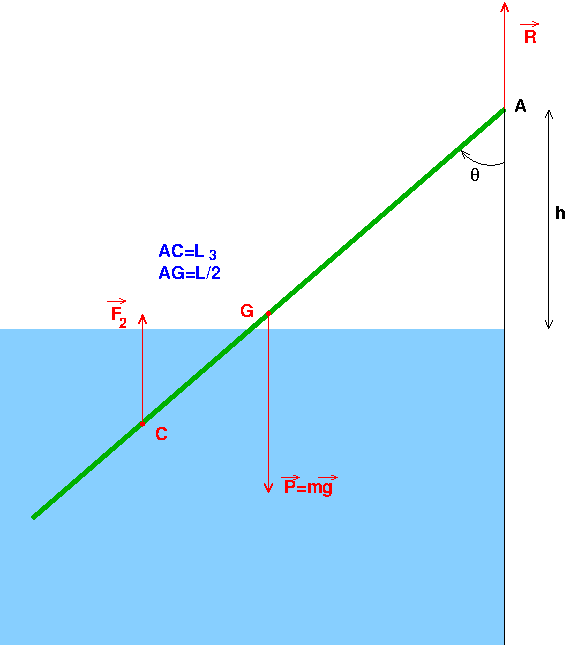
 défini sur mon schéma qui n'est pas celui de l'énoncé mais son complémentaire.
défini sur mon schéma qui n'est pas celui de l'énoncé mais son complémentaire.

