Inscription / Connexion Nouveau Sujet
Problème électricité
Bonjour,
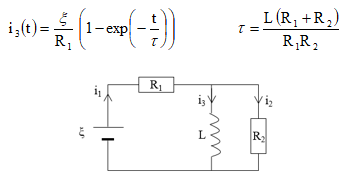
J'ai un problème avec ce circuit, je dois déterminer l'intensité dans la branche comportant la bobine mais je suis embêté parce que cette bobine est en parallèle avec la résistance droite (R2) et le tout est en série avec la résistance du haut (R1). Donc je suis bloqué car en utilisant les 2 lois de Kirchhoff je n'arrive pas du tout à obtenir les expressions demandées dans l'énoncé (on demande de montrer que l'intensité et la constante de temps du circuit prennent les formes indiquées)
J'ai fait cela :
Loi des noeuds : i1=i2+i3
Loi des mailles : uL=u2 et E-u1-uL=0
On obtient donc en utilisant la loi de fonctionnement de la bobine,
L*(di1/dt)+R1*i1=E
Mais je n'arrive pas à me débarasser de i1, si j'utilise la loi des noeuds alors c'est i2 qui va intervenir...
Pouvez-vous SVP me guider ?
Merci!
Bonjour,
Il faut bien en effet utiliser la loi des noeuds et vous débarrasser de i2 ensuite à l'aide de uL=u2.
Merci !
D'accord mais en faisant cela je tombe sur :
i1=i2+i3 Soit i3 = i1 - i2 = i1 - u2/R2 = i1 - uL/R2 = i1 - (L/R2)*di3/dt
Soit (L/R2)*di3/dt + i3 = i1
Il reste donc i1... Si ce n'est pas i1 c'est i2, je suis un peu perdu
i1=i2+i3 Soit i3 = i1 - i2
Là vous tournez en rond, il n'est pas question de réécrire i3 puisque c'est l'inconnue mais i1, dont on veut se débarrasser, :
Merci pour votre réponse,
Oui j'ai bien conscience de cela, et c'est d'ailleurs l'expression que j'ai notée sur mon précédent message, mais on ne peut rien tirer de cela car i1 subsiste. L'équation différentielle ne peut être résolue sans une expression alternative de i1
Merci pour votre aide
Vous avez votre équation de départ :
dans laquelle vous remplacez i1 par sa valeur obtenue par la loi des noeuds :
Il ne reste plus qu'une seule variable i3.
Et sinon, vous connaissez Thévenin Norton et le diviseur de tension ?
Cela allège considérablement les calculs.
Merci beaucoup pour votre aide, j'ai compris ce que vous avez expliqué.
Je connais le diviseur de tension mais je ne vois pas comment il pourrait s'appliquer ici, à cause de la bobine ? Sans utiliser la formalisme des impédances
Pour Thévenin Norton j'ai commencé à m'y intéresser mais je ne suis pas encore opérationnel à 100%.
A quoi auriez-vous pensé en utilisant ces méthodes ?
On isole E,R1,R2 et on cherche le générateur de Thévenin équivalent et de résistance
et on a un simple circuit {e,R,L}.
J'ai pu le faire grâce à vos conseils en utilisant le théorème de Thévenin et je tombe bien sur le résultat demandé. Toutefois si je ne m'abuse, la tension de Thévenin est E*R2/(R1+R2) et non pas E*R1/(R1+R2)
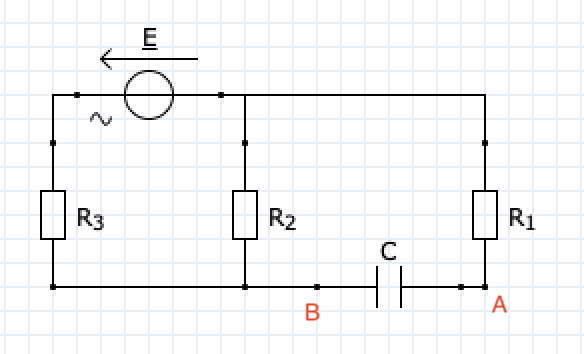
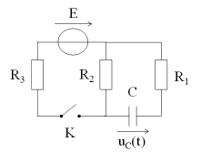
J'ai essayé d'employer la même méthode dans le montage ci-dessous, pour déterminer la tension aux bornes de la capa lorsque celle-ci se charge (interrupteur fermé). J'ai tenté la méthode traditionnelle (Kirchhoff) mais impossible d'y arriver, je tourne en rond parce que j'ai l'impression d'avoir + d'inconnues que de relatioins. Pareil pour Thévenin. Auriez-vous une piste à me proposer ?
La décharge du condensateur (interrupteur ouvert) dans les 2 résistances R1 et R2 est elle triviale.
Par Thévenin, on isole le générateur (E R3 R2) et on applique la méthode précédente.
Par Thévenin, il n'y a pas de raison de séparer (R1 C) qui forme un seul dipôle.
Sinon
- 4 inconnues i1, i2, i3 et uC
- donc 4 équations : loi des noeuds, loi de la capacité et 2 lois de maille.
Vous avez raison, j'avais mal géré mes équations et je suis finalement parvenu à former l'équation différentielle d'évolution de uC. L'équation est vraiment lourde cependant.
N'est-il pas possible de former une résistance équivalente à R3 et R2 ?
Celles-ci sont disposées en parallèle si je ne m'abuse ; par contre comment cette résistance équivalente serait-elle disposée par rapport à la maille de droite ?
Et je n'ai pas saisi ce que vous avez dit à propos de Thévenin : puisqu'on cherche la tension entre uC, pourquoi inclure la résistance R1 dans le dipôle ?
Je voulais dire que pour chercher le schéma équivalent, il était plus simple de chercher l'équivalent de (E R3 R2) puis brancher le dipole (R1 C). Mais il est à peine plus lourd de prendre (E R3 R2 R1) puis brancher C.
Vous obtenez (R2 // R3) + R1.
Je m'absente, et pour répondre plus proprement il faut un dessin donc un peu plus de temps. Donc suite plus tard.
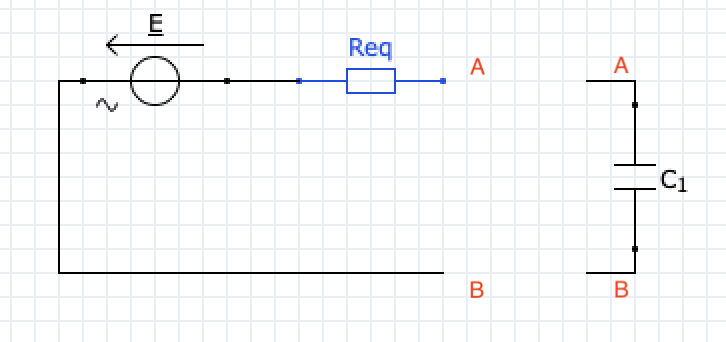
Point de départ :
On coupe le circuit en 2 en A et B.
Ce qui donne :
Puis on applique Thévenin à gauche ce qui donne entre autres comme résistance équivalente :
On a bien (R3 // R2) + R1
Il n'y a plus qu'à reconnecter :
Les points A et les points B.
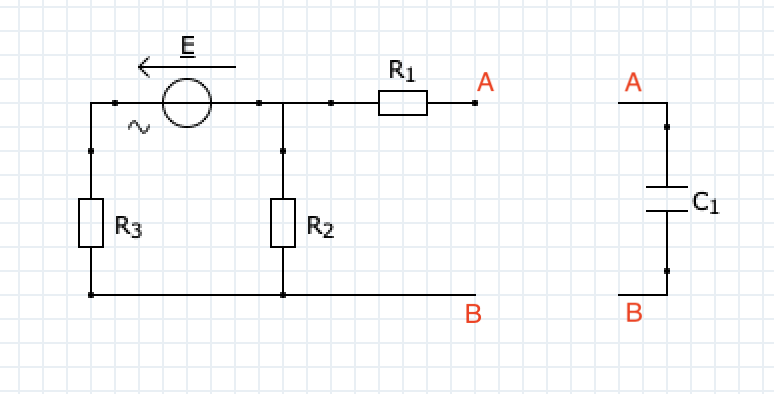
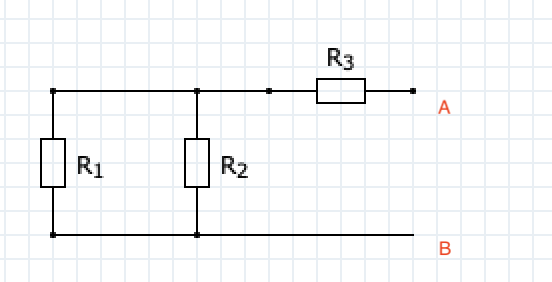
Merci beaucoup pour ce travail, par contre la fem n'est pas dans le bon sens (même si ce n'est qu'arbitraire...) et je me demandais également comment calculer la fem de Thévenin dans ce cas ? Pour la résistance Rth c'est bon mais pour la tension de Thévenin j'ai encore un peu de mal car le diviseur de tension ne semble pas s'y prêter...?
pour la tension de Thévenin j'ai encore un peu de mal car le diviseur de tension ne semble pas s'y prêter.
C'est bien pour cela que j'avais indiqué initialement une coupure (E R3 R2) (R1 C) pour que l'on tombe sur qqch de connu.
La détermination du générateur de Thévenin se fait en cherchant la fem qui est la tension à vide, donc avec un courant de sortie nul, il n'a donc pas de courant dans R3, donc une chute de tension nulle aux bornes de R3, et la tension sera donc donnée par le diviseur de tension (E R3 R2).
Bonjour,
@pulsar80 : pourrais-tu mettre à jour ton profil stp ?
 extrait de
extrait de Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau topic ?
Ce dernier indique terminale S quand tu postes dans le supérieur (licence) : qui a raison ?
C'est bien pour cela que j'avais indiqué initialement une coupure (E R3 R2) (R1 C) pour que l'on tombe sur qqch de connu.
La détermination du générateur de Thévenin se fait en cherchant la fem qui est la tension à vide, donc avec un courant de sortie nul, il n'a donc pas de courant dans R3, donc une chute de tension nulle aux bornes de R3, et la tension sera donc donnée par le diviseur de tension (E R3 R2).
Très bien, merci énormément, je pense avoir compris !
@gbm désolé je n'avais pas compris, j'ai bien un niveau terminale S car je viens d'avoir mon bac mais je suis inscrit en licence. Je pensais qu'il s'agissait du dernier diplôme obtenu, mes excuses, je modifie mon profil

 équivalences des systèmes de niveaux scolaires
équivalences des systèmes de niveaux scolaires
