Inscription / Connexion Nouveau Sujet
Problème de mécanique des fluides
Bonsoir tout le monde,
Alors voilà cela fait 3 jours que je galère sur cet exercice :
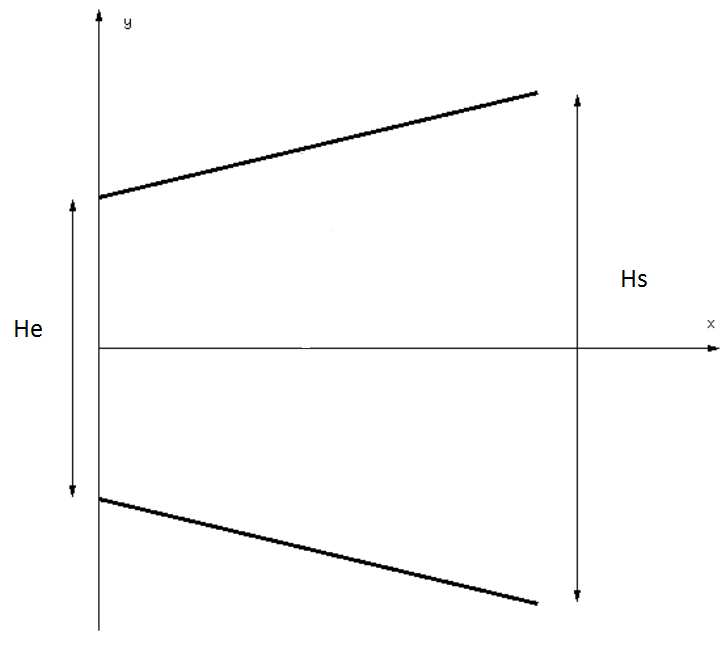
Il s'agit d'étudier un écoulement bidimensionnel entre deux parois planes distantes d'une fonction H(x) sur une longueur L. On connait l'arrête d'entrée He et l'arrête de sortie Hs. La distribution des vitesses est donnée par : U(x,y)=A(x)cos( *y/H(x)). On connait A(x) en 0 : U0 et en L 0.9*U0. La question est de déterminer l'augmentation de pression sur la longueur L, sachant que cette variation de pression est linéaire : p = pe + A((y-1)/2He) avec A à déterminer. (pe : pression d'entrée)
*y/H(x)). On connait A(x) en 0 : U0 et en L 0.9*U0. La question est de déterminer l'augmentation de pression sur la longueur L, sachant que cette variation de pression est linéaire : p = pe + A((y-1)/2He) avec A à déterminer. (pe : pression d'entrée)
Le frottement est négligé.
J'ai essayé de passer par le bilan de masse, la conservation des débits et bilan de quantité de mouvement pour faire apparaitre la pression et essayer de trouver une forme linéaire pour faire une identification mais j'avoue que je me suis un peu perdu et je sèche...
Si quelqu'un pourrait me donner un petit coup de pouce, cela serait génial.
Merci d'avance, et un joyeux noel en retard à tous ! 
oui ça pourrait être une bonne idée de rentrer ça dans l'équation de quantité de mouvement par exemple, puisque tu as les expressions de la vitesse et de la pression. L'écoulement est incompressible j'imagine ?
oui il est incompressible et stationnaire
pour appliquer l'équation de quantité de mouvement on a besoin des normales aux surfaces c'est là où j'ai un problème j'ai déduit que les normales aux parois avait comme coordonnées N1 (- sin a / cos a ) pour la supérieur et N2 (-sin a / -cos a) est-ce que vous êtes d'accord avec ça ?
Merci de votre aide
on peut prendre x parallèle à une paroi non ?
donc il faut juste la normale à la paroi supérieure : (-H'(x); 1)
on te l'impose ? sinon on pourrait prendre l'axe x confondu avec la paroi du bas. Et on ne dit pas que H(x) est une fonction linéaire. D'ailleurs à quoi vont te servir les normales aux parois ?
schéma imposé. Bah je comptais appliquer la formule suivante : 

 (
( .n)dS = Fe
.n)dS = Fe
avec Fe = forces extérieurs : poids du fluide 
 gdv, pression du fluide
gdv, pression du fluide  -P*ndS , et Fs forces exercées par les parois sur le fluide
-P*ndS , et Fs forces exercées par les parois sur le fluide
Je vois que ça pour trouver la pression.
J'ai aussi raisonner avec la conservation des débits : U1He = U2Hs mais je sais pas continuer.
Qu'en dis-tu ?
Merci 
oui tu peux calculer H1 et H2
par contre, pourquoi tu n'utilises pas l'équation d'Euler pour la quantité de mouvement ?
 (
( .grad)
.grad)  = - grad p
= - grad p
Ah oui en effet c'est plus simple vu de cette façon,
par contre par exemple pour le calcul de U1, on fait U(0,y)=U0cos( *y/He) après je vois pas quoi faire. on calcul le débit ?
*y/He) après je vois pas quoi faire. on calcul le débit ?
Merci 
oui il faut calculer le flux de U à travers He et Hs
essaie de calculer les projections sur x et y de l'équation d'Euler
alors pour U(0,y).dy je trouve : -2*He/pi * U0 (normale orienté vers l'ext)
et U(L,y) = 1.8*HS /pi * U0
et apres je ne vois pas comment appliquer les équations ...
Bah selon l'énoncé on a bien U(x,y) mais je pense que oui c'est suivant x en tout cas c'est prépondérant selon moi
bon je te passe les calculs, tu es censé pouvoir les faire mais on tombe sur :
U.dU/dx + V.dU/dy = 0
U.dV/dx + V.dV/dy = - dp/dy
les dérivées sont des dérivées partielles évidemment et V est la composante selon y de la vitesse (si on la prend nulle tu vois que ça ferait des choses bizarres donc essayons comme ça)
la première équation devrait permettre de trouver V(x,y) puisqu'il y a juste à remplacer U
ainsi on connaitra le membre de gauche de la deuxième équation et on pourra trouver dp/dy donc A
à toi de jouer
c'est sans doute à cause de l'heure tardive mais dU/dx ça me donne un gros truc barbare du style A'cos(pi*y/H) + A* (pi*sin(pi*y/H)y(dH/dx)/H(x)²
je pense que je dois me gourrer 
hum si ça a l'air d'être ça mais c'est pas beau effectivement ^^ tu es sur que les parois s'écarte linéairement entre l'entrée et la sortie ? ça permettrait de calculer facilement H(x)
non j'ai vraiment aucunes infos là dessus.
Merci encore pour ta patience et ton aide en tout cas 
on a 1/2 de H(x) de chaque côté je sais pas si ça peut servir.
oui mais si on considères que H(x) est une fonction affine, alors on aurait H(x)=(Hs-He)x/L + He ça serait plus simple ^^
bon désolé je vais me coucher, j'essaierai de refaire les calculs demain soir pour voir si on peut trouver qque chose d'intéressant
Alors j'ai re-réfléchi et ça donne vraiment des résultats trop énorme je pense : pourquoi pas essayer avec Bernoulli entre He et Hs sur la ligne de courant y = 0 on néglige l'altitude et on obtient :
Ps - Pe = 1/2 *  * (Ue²-Us²)
* (Ue²-Us²)
Ue = U0²
Us = 0.9²*U0²
d'ou Ps-Pe = 1/2 * *U0²*0.19
*U0²*0.19
après calculs et identification je trouve A = - *He*0.19*U0²
*He*0.19*U0²
Ça m'embête dans la mesure où on est pas sensé trouver une constante positive ?