Niveau licence

Problème de Kepler

Posté par
DeuxNids 10-02-17 à 20:46

Bonsoir tout le monde,

Alors j'ai un petit problème de compréhension dans un de mes cours de méca...

Pour situer le truc, c'est pour la résolution du problème de Kepler (à 2D) donc on étudie un objet en mouvement qui va subir une force centrale et qui va donc avoir un mouvement circulaire ou elliptique.
Pour étudier tout ça on se place en coordonnées polaires $(r,\theta)$ .

L'objet est situé au point $M(r,\theta)$ , et en ce point on a donc une base mobile $(\overrightarrow{e_r},\overrightarrow{e_\theta})$ .

On calcule d'abord la vitesse de l'objet :
$\frac{d\overrightarrow{r}}{dt}=\dot{r}\overrihtarrow{e_r}+r\dot{\overrightarrow{e_r}}$

Et le problème est dans la relation suivante :
$\dot{\overrightarrow{e_r}}=\frac{d\overrightarrow{e_r}}{dt}=\frac{d\overrightarrow{e_r}}{d\theta}\frac{d\theta}{dt}=\dot{\theta}\overrightarrow{e_\theta}$

Comment on justifie le fait que $\frac{d\overrightarrow{e_r}}{d\theta}=\overrightarrow{e_\theta}$ ??

Merci d'avance pour votre aide

Posté par re : Problème de Kepler 10-02-17 à 21:46

Hello

C'est à dessein que j'utilise des notations différentes:

$\vec{u} \left( \begin{array}{c} \\ cosx \\ \\ sinx \\ \end{array} \right)$

Soit $\vec{v} = \frac{d\vec{u}}{dx}$

$\vec{v} \left( \begin{array}{c} \\ -sinx \\ \\ cosx \\ \end{array} \right)$

J'ai bien fait une rotation de $+\frac{\pi}{2}$ en passant de $\vec{u}$ à $\vec{v}$

C'est bon?

Posté par re : Problème de Kepler 10-02-17 à 22:37

Ah oui merci c'est beaucoup plus clair !

Mais il y a encore une petite chose qui me perturbe... Quand je place mon vecteur $\overrightarrow{u}$ sur un cercle trigo, et que je place aussi le vecteur $\overrightarrow{v}$ , pour moi le vecteur $\overrightarrow{v}$ est décalé de $-\frac{\pi}{2}$ puisqu'on a un $(-sinx)$ dans $\overrightarrow{v}$ . Et du coup dans le cas de mon problème j'aurais plus tendance à écrire $\frac{d\overrightarrow{e_r}}{d\theta}}=-\overrightarrow{e_\theta}$ .

Je ne vois pas où est mon erreur alors qu'elle est bien là :/

Posté par re : Problème de Kepler 11-02-17 à 05:59

hum hum, je ne vois pas non plus où se situe ton erreur ...

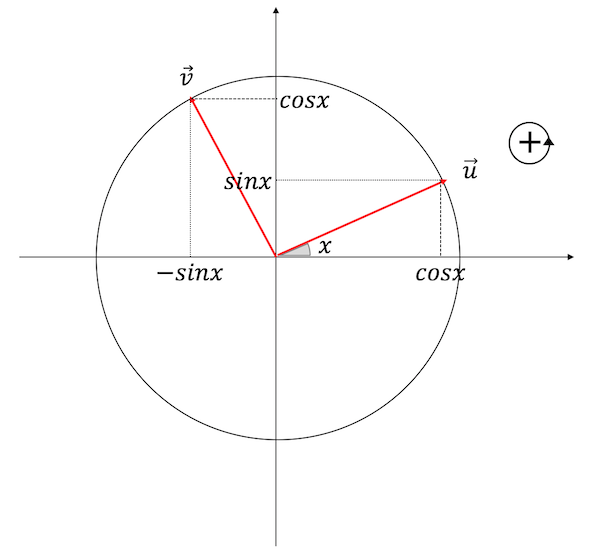
Un dessin pour servir mon dessein?

On tourne bien de $+\frac{\pi}{2}$ pour aller de $\vec{u}$ à $\vec{v}$

Problème de Kepler

Posté par re : Problème de Kepler 11-02-17 à 16:45

Ah oui c'est bon !!

Je m'obstinais à mettre le $-sinx$ sur l'axe des ordonnées..

C'est bon du coup problème réglé, merci beaucoup dirac !

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Problème de Kepler

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique