Niveau maths spé

Problème de convolution

Posté par
CHOUEB 18-06-10 à 21:15

Bonjour à tous,

voilà j'ai un petit problème qui se pose à moi, j'espère que vous pourrez m'aider, j'en ai bien besoin:
Sujet:
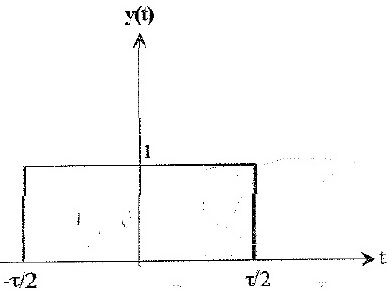
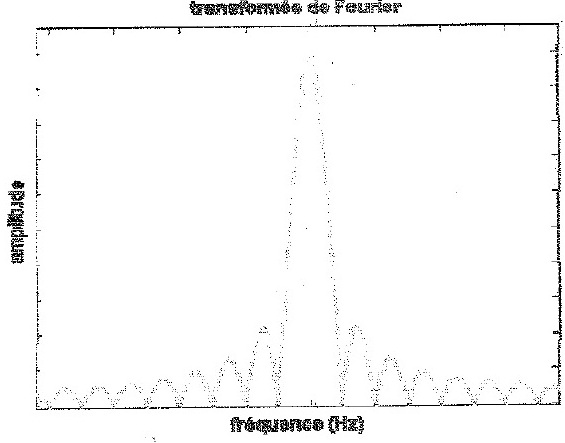
On rappelle que la transformée de fourrier de la fonction rectangle (porte) de largeur 1 est donnée par:
TF((t)) = .sin(.f.)

- Par raisonnement graphique, et en utilisant les propriétés de symétrie, calculer le produit de convolution de la fonction rectangle par la largeur 1 (=1) par elle-même.
Représenter graphiquement les signaux x() et x(t-) et faire le calcul pour =0 , 1/2 , 3/2 , 2

on donne ces 2 graphiques en complément.

- En déduire une autre façon de calculer la transformée de fourrier.

Si quelqu'un pouvait m'aider je lui en serais fort reconnaissant.
Merci par avance.

Problème de convolution

Posté par re : Problème de convolution 19-06-10 à 00:51

Pas tres compliqué mais quand meme pas évident.
Ta porte n'est pas juste et le x va de -1/2 a +1/2
Ecris l'intégrale de convolution. Il y a deux portes comme intégrand. La première te limite l'intervalle d'intégration de -1/2 à +1/2
Fais ensuite un changement de variable pour la seconde porte (x-)= (y) alors d=-dy et les bornes vont de x+1/2 à x-1/2 avec le signe - ca s'inverse.
Apres reflechis sur l'integrale (y) vaut 1 dans l'intervalle -1/2 à + 1/2. Par conséquant
- tant que la borne superieure x+1/2 n'atteint pas -1/2 l'intégrale est nulle
-fais avancer ton segment d'intégration, dés qu'il penetre dans la porte ton integrale te donne une droite positive
- le max est lorsque le segment est tout entier dans la porte
la ca fait 1
- on avance le segment (x-1/2, x+1/2) on a une droite qui descend
- l'intervalle d'integration est ressorti l'integrale est de nouveau nulle.
OUAH ca fait un triangle !!

La seconde question est nulle. ()=²()