Niveau iut

problème de calcul régime sinusoïdal

Posté par
lotus18 15-12-17 à 22:25

Bonjour,
voici la consigne d'un exercice que je réussis pas:
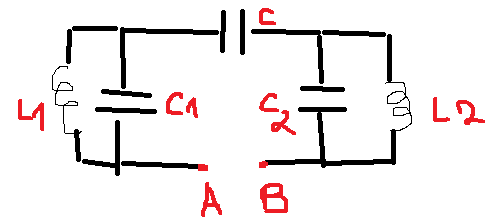
trouver l'impédance complexe puis réelle aux bornes de ce dipôle.
Montrer que quand w = w1 ou w = w2, le courant ne passe pas.
1/\sqrt{L1*c1} = w 1
1/\sqrt{L2*c12} = w 2

Le problème c'est que pour tous les exercices en régime sinusoidal j'ai des problèmes de calculs. Ici j'ai l'impression que le numérateur final n'est pas homogène mais je ne sais pas quelle grandeur attribuer au 1.
Je sais que mon résultat est faux, en effet je devrais trouver que mon dénominateur tend vers l'infini quand w tend vers w1 ou w tend vers w2, or avec mon dénominateur ce n'est pas possible. Mais je n'arrive pas à trouver mes fautes. De façon général, y a t-il des astuces ou des méthodes à suivre pour alléger les calculs ou les simplifier très rapidement car souvent dans les corrections, l'expression finale est relativement simple alors que  dans mes expressions à moi , pas du tout.
Voilà ce que j'ai trouvé:

\frac{ZL1*Zc1}{ZL1+Zc1} +\frac{ZL2*Zc2}{Zl2+Zc2} +Zc
    = L1/c1 *\frac{jc1w}{-w1*w^{2+1}}+L2/c2*\frac{jc2w}{-w1*w^{2}+1}+ 1/jcw
=\frac{w1^{2}jw}{c1*(-w1*w^{2}+1)}+  \frac{w2^{2}jw}{c2*(-w2*w^{2}+1)} +1/j*c*w =
\frac{c2*w1^{2}*jcw
}{c2*c1*jc*w*(-w1*w^{2}+1)}   +  \frac{c1*w2^{2}*jcw
}{c2*c1*jc*w*(-w1*w^{2}+1)}+      \frac{ c1*c2*(-w2*w^{2}+1 }{c2*c1*jc*w*(-w1*w^{2}+1}
Merci par avance

problème de calcul régime sinusoïdal

Posté par re : problème de calcul régime sinusoïdal 15-12-17 à 22:30

$\frac{ZL1*Zc1}{ZL1+Zc1} +\frac{ZL2*Zc2}{Zl2+Zc2} +Zc = L1/c1 *\frac{jc1w}{-w1*w^{2+1}}+L2/c2*\frac{jc2w}{-w1*w^{2}+1}+ 1/jcw =\frac{w1^{2}jw}{c1*(-w1*w^{2}+1)}+ \frac{w2^{2}jw}{c2*(-w2*w^{2}+1)} +1/j*c*w = \frac{c2*w1^{2}*jcw }{c2*c1*jc*w*(-w1*w^{2}+1)} + \frac{c1*w2^{2}*jcw }{c2*c1*jc*w*(-w1*w^{2}+1)}+ \frac{ c1*c2*(-w2*w^{2}+1 }{c2*c1*jc*w*(-w1*w^{2}+1}$

je le reposte car je ne sais pas pourquoi çà n'est pas lisible

Posté par re : problème de calcul régime sinusoïdal 15-12-17 à 22:57

Bonsoir
Tu as bien compris physiquement les associations de dipôles mais tu te montres maladroit dans les calculs. Je vais t'aider pour l'association (L1//C1) ; il te sera facile de transposer à (L2//C2) puis de terminer...

$\frac{ZL1*Zc1}{ZL1+Zc1}=\frac{ZL1}{1+\frac{ZL1}{ZC1}}=\frac{jL_{1}\omega}{1-L_{1}C_{1}\omega^{2}}$

Selon l'énoncé : $L_{1}C_{1}\omega_{1}^{2}=1$ donc :

$L_{1}C_{1}\omega^{2}=\left(\frac{\omega}{\omega_{1}}\right)^{2}\quad;\quad\frac{ZL1*Zc1}{ZL1+Zc1}=\frac{jL_{1}\omega}{1-\left(\frac{\omega}{\omega_{1}}\right)^{2}}$

Je te laisse continuer... Il te sera facile de montrer ensuite que, pour $\frac{\omega}{\omega_{1}}=1$ ou pour $\frac{\omega}{\omega_{2}}=1$ l'impédance tend vers l'infini : aucun courant ne passe.

Posté par re : problème de calcul régime sinusoïdal 16-12-17 à 22:01

Merci beaucoup. Mais comment as tu su que le fait de diviser par Zc1 allait simplifier les calculs par la suite ? De plus comment as tu pensé à faire cette égalité à 1 ?puis à poser w/w1 par ce que c'est vraiment typiquement le genre de chose avec lesquelles j'ai des problèmes

Posté par re : problème de calcul régime sinusoïdal 16-12-17 à 22:28

Quelques années d'entraînement!
Deux conseils souvent utiles :
En présence de L et C, essaie de faire apparaître des termes en LC² grandeur sans dimension qui, pour une fréquence telle que LC²=1 conduit souvent à des propriétés remarquables du circuit.
En présence de R et C, essaie pour la même raison de faire apparaître des termes en RC...

Posté par re : problème de calcul régime sinusoïdal 17-12-17 à 14:23

D'accord. Mais pourquoi sont ils sans dimension ?

Posté par re : problème de calcul régime sinusoïdal 17-12-17 à 14:50

Je pars de formules simples que tu connais et le note entre crochets la dimension physique de la grandeur:

$u=-L\frac{di}{dt}\quad;\;\;L=-\frac{u}{\frac{di}{dt}}$
La dimension physique de L est :
[L]=[U].[T].[I]^-1
Une inductance est homogène au produit d'une tension par un temps, le tout divisé par une intensité.
L'intensité de charge d'un condensateur peut s'écrire :

$i=C\frac{du}{dt}\quad;\quad C=\frac{i}{\frac{du}{dt}}$
La dimension physique de C est :
[C]=[I].[T].[U]^-1
une capacité est homogène au produit d'une intensité par un temps, le tout divisé par une tension.

$\omega^{2}=\left(\frac{2\pi}{T}\right)^{2}$
La dimension physique de $\omega^{2}$ est :
$\\ \left[\omega^{2}\right]=\left[T\right]^{-2}$
Le carré d'une pulsation a pour dimension l'inverse du carré d'un temps.
Ainsi la dimension physique de $LC\omega^{2}$ est :

$\left[LC\omega^{2}\right]=\left[U\right]\left[T\right]\left[I\right]^{-1}\cdot\left[I\right]\left[T\right]\left[U\right]^{-1}\cdot\left[T\right]^{-2}=1$

$LC\omega^{2}$ est bien une grandeur sans dimension, ou, si tu préfères, une grandeur de dimension 1. Je te laisse démontrer, par une méthode analogue que $RC\omega$ est aussi une grandeur sans dimension.