Inscription / Connexion Nouveau Sujet
Problème conversion
Bonjour, j'ai pas un problème sur les conversions de températures et pourtant je sais que c'est basique.
T(K)=T(°C)+273
Et diff de T en K = diff de T en °C
Et pourrant en le faisant avec un exemple je bloque.
Ex:
T1=T2-T3
Avec T1=1000°C, T2=1100°C et donc T3=100 °C
En convertissant (même si je sais qu'un diff de T ne devrait pas dépendre de celsisus ou kelvin:
T1=1000+273, T2=1100+273; T3= 100+273 et donc
T1=1273 et T2-T3=1000 alors l'égalité ne correspond plus.
Merci d'avance
Bonjour
Il ne faut pas ajouter 273 à T3 puisqu il s'agit d'une différence de température.
Conseil pour plus de clarté : utiliser la lettre T pour les températures en kelvins et t pour celles en °C.
Histoire de faire cela proprement :
Situation 1 :
Situation 2 :
Évidemment :
Ne pas désigner la différence de températures par un symbole habituellement réservée à une température ; c'est sans doute cela qui t'a piégé. Utiliser par exemple la notation  T ou
T ou  t.
t.
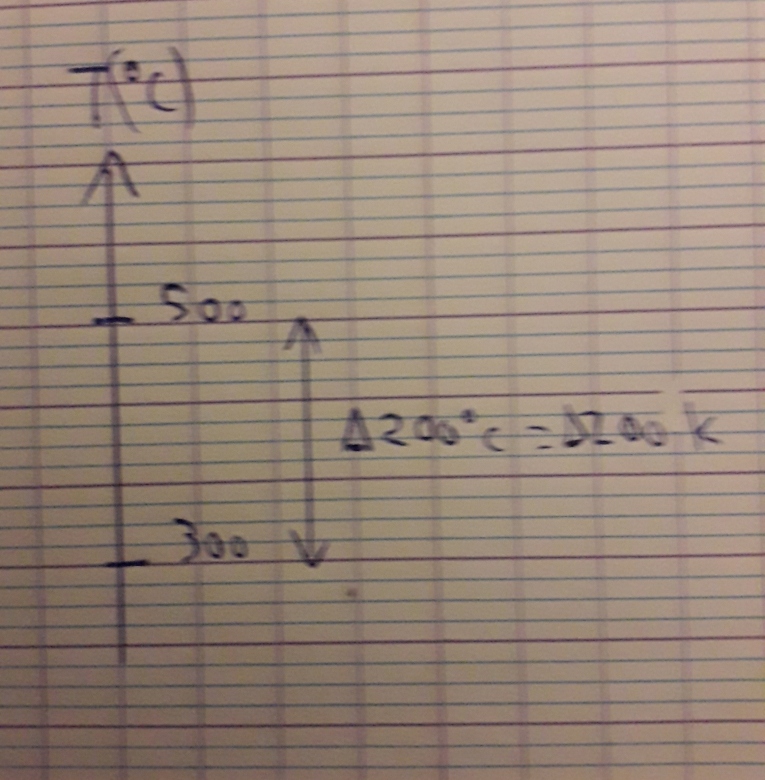
T1= 1273K
T2-T3=(1100-100)+273 K
Mais si maintenant on a:
TA=TB-x/y
Avec comme valeur:
- pour x: 1500W/m
-pour y: 15W/m/K
-pourTB:250°C
On aura alors TA=250°C-100K
Et là j'hésite, pour moi je devrais convertir 100 K en °C alors qu'il ne le faut pas et donc TA=150°C
Il ne faut pas ajouter 273 à T3 puisqu il s'agit d'une différence de température.
L'erreur ne vient pas du fait qu'il faut d'abord tout sommer et ensuite convertir ?
Réponse à ton message de 19h27 :
Dès qu'il s'agit d'exprimer une différence ou une variation de température, le degré Celsius et le kelvin sont deux unités équivalentes. On peut utiliser l'une où l'autre au choix. Par exemple, une capacité thermique est le rapport (quantité de chaleur reçue/variation de température correspondante) ; elle peut s'exprimer indifféremment en J/°C ou en J/K. Je me permet de citer le texte officiel sur le sujet, publié par le Bureau International des Poids et Mesures : "L'unité de température Celsius est le degré Celsius, symbole °C, qui par définition est égal en amplitude à l'unité « kelvin ». Une différence ou un intervalle de température peut s'exprimer aussi bien en kelvins qu'en degrés Celsius, la valeur numérique de la différence de température étant la même dans les deux cas. "
Mon message de 17h10 corrige ton premier message. Evidemment dès qu'intervient un quotient, plus question d'utiliser l'échelle Celsius. Un rapport de deux températures repérées dans l'échelle Celsius n'a aucun sens physique. En cas de doute, je te conseille de faire tous les raisonnements et calculs intermédiaires en kelvins, quitte si nécessaire à exprimer le résultat final dans l'échelle Celsius.
C'est un peu plus clair, merci.
Est-ce que c'est correct:
T=500 °C - 100K = 400 °C (=400K) ou bien avant la soustraction je dois convertir 500°C en K ou convertir 100K en °C ?
Oui, en fait c'est bon j'ai compris.
T1(°C)=T2(°C)-T3(K)
Il faut bien évidemment convertir T3 en °C.
Par contre pour le cas TA(°C)=TB(°C)-x/y (K), il ne faut pas convertir le rapport x/y en °C car W/m/K signifie que la puissance qu'il faut fournir par mètre pour une variation de température et donc vu que c'est une variation: W/m/K=W/m/°C
Merci beaucoup !
Je pense que tu l'as compris maintenant mais je préfère le préciser : ton message de 20h28 est faux. Une différence de températures a même valeur dans les deux échelles mais les températures que l'on soustrait doivent être repérées dans la même échelle. Si tu as le moindre doute, raisonne dans l'échelle Kelvin.