Inscription / Connexion Nouveau Sujet
Problème cinématique
Bonjour à tous, j'ai commencé un exercice de cinématique et je n'arrive pas du tout à le résoudre, je ne veux pas la réponse, j'aimerai juste avoir la méthode pour le faire 
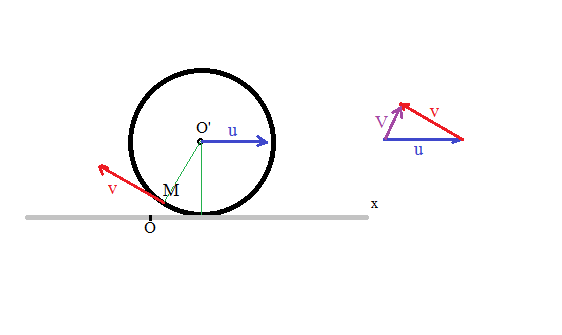
Roulement sans glissement. On considère dans le plan un axe fixe Ox. Une roue circulaire de centre O' et de rayon R roule sans glisser sur Ox, de sorte que la vitesse O' soit u = 1 m/s. On donne : R = 0,5 m.
1. A l'instant t=0 un point M de la roue est en O. Calculer l'angle que fait le vecteur vitesse du point M avec Ox pour t = 0,1 s et t = 1 s. On donnera le résultat en degrés et minutes.
2. Même question pour le vecteur accélération.
3. Quelle est la valeur maximale du module de la vitesse?
je vous remercie de votre aide 
1 et 2)
Je le fais pour t = 0,1 s.
Vitesse angulaire de la roue autour de O' : w = u/R = 1/0,5 = 2 rad/s
En t = 0,1 s, la roue a donc tourné d'un angle alpha = 2 * 0,1 = 0,2 rad
Le vecteur vitesse v de M (autour de O') est perpendiculaire au rayon OM et v = 1 m/s
L'angle que fait le vecteur v avec Ox est aussi de 0,2 rad.
Le vecteur vitesse V de M est la somme des vecteurs u et v
vecteur u (1 ; 0)
vecteur v (-1*cos(alpha) ; 1.sin(alpha))
vecteur V (1 - cos(alpha) ; 1 . sin(alpha))
vecteur V (0,0199 ; 0,199)
Soit Beta l'angle entre vecteur V et ox : 0,199 = 0,0199*tan(Beta)
Beta = 1,47 radian = 84°17min
vx = 1 - cos(alpha)
Vy = sin(alpha)
Vx = 1 - cos(2.t)
Vy = sin(2.t)
dVx/dt = 2.sin(2t)
dVy/dt = 2.cos(2t)
et en t = 0,1 s : vecteur a (2*sin(0,2) ; 2.cos(0,2))
vecteur a (0,397 ; 1,96)
Soit Gamma l'angle entre vecteur a et ox : 1,96 = 0,397.tan(Gamma)
Gamma = 1,371 rad = 78°33min
-----
Calculs non vérifiés ...
---> A vérifier et recommencer avec t = 1 s
----------
3)
Vx = 1 - cos(2.t)
Vy = sin(2.t)
|V|² = (1 - cos(2t))² + sin²(2t)
|V|² = 1 + cos²(2t) - 2.cos(2t) + sin²(2t)
|V|² = 2 - 2.cos(2t)
|V|² = 2(1 - cos(2t))
|V|² est max (et donc |V| aussi) si cos(2t) = - 1
|V|² max = 4
|V|max = 2 m/s
C'est pour 2t = Pi + 2k.Pi, doncc pour t = Pi/2 + k.Pi (k entier)
Donc pour des angles alpha = Pi + 2k.Pi ... donc chaque fois que M est "au plus haut" de la roue par rapport à la route. (mais n'était-ce pas évident ?).
-----
Le tout à vérifier ...



