Inscription / Connexion Nouveau Sujet
probleme calcul d'une intensité
Bonjour,
je suis bloquée sur un exo d'élec.
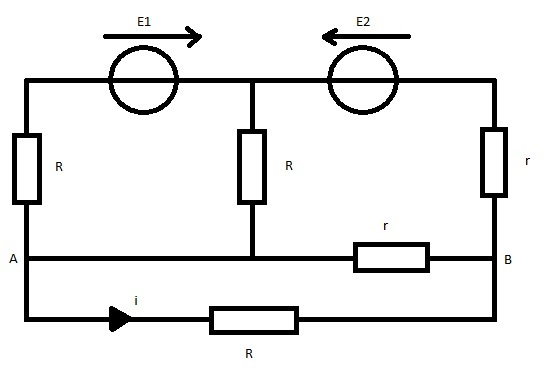
Je dois calculer littéralement i circulant dans R entre A et B comme sur l'image jointe mais je ne vois pas comment placer les autres intensités partant de E1 et E2 vu qu'ils sont "opposés".
bref si quelqu'un peut me donner un petit coup de main ça serait pas de refus 
Bonsoir,
i=(UA-UB)/R
Reste à trouver UA et UB
Je te propose de donner un nom, C, au point de jonction en haut entre E1, E2 et R.
Tu peux écrire les équations des courants aux noeuds A, B et C:
Sauf erreur, tu as
En A:
(UC-UA)/R+(UC-E1-UA)/R+(UB-UA)(1/r+1/R)=0
En B:
(UC-E2-UB)/r+(UA-UB)((1/r+1/R)=0
En C:
(UC-E1-UA)/R+(UC-E2-UB)/r-(UC-UA)/R=0
Ce qui te donne 3 équations à 3 inconnues (UA, UB et UC)
Y'a plus qu'à! 
j'ai demandé a ma prof qui m'a dit de placer deux intensités (i1, i2) chacune sortant d'un générateur en respectant la convention générateur, l'intensité dans la résistance R est alors i1 + i2. mais après je vois pas comment je dois placer les autres ?! (celle qui repart de A vers E1 c'est quoi? de meme pour B vers E2)
Tu as donc le choix:
Ce que t'a proposé ta prof: Sans doute, ça marche.
Ce que je t'ai proposé: Très probablement, ça marche aussi.
Tu fais comme tu veux!
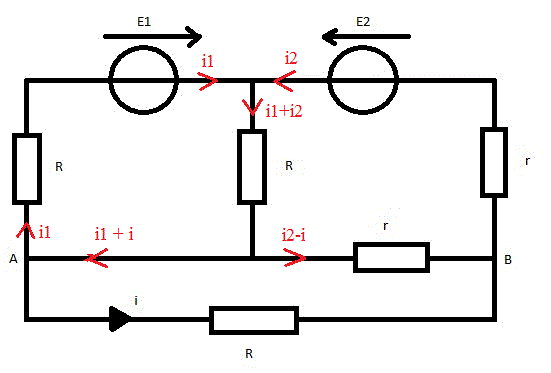
3 équations de mailles :
E1 - R(i1 + i2) - R.i1 = 0
E2 - R(i1 + i2) - r.(i2-i) - r.i2 = 0
r(i2-i) - R.i = 0
E1 - 2R.i1 - R.i2 = 0
E2 - Ri1 - i2(R + 2r) + ri = 0
r.i2 - (r+R)i = 0
i2 = [(r+R)/r].i
E1 - 2R.i1 - R.[(r+R)/r].i = 0
E2 - Ri1 - [(r+R)/r](R + 2r).i + ri = 0
i1 = E1/(2R) - [(r+R)/(2r)].i
i1 = E2/R - [(r+R)/(Rr)].(R + 2r).i + (r/R)i
E1/(2R) - [(r+R)/(2r)].i = E2/R - [(r+R)/(Rr)].(R + 2r).i + (r/R)i
r.E1/(2Rr) - [R.(r+R)/(2Rr)].i = 2rE2/(2rR) - [2(r+R)/(2Rr)].(R + 2r).i + (2r²/(2rR)).i
r.E1 - R.(r+R).i = 2rE2 - 2(r+R).(R + 2r).i + 2r².i
r.E1 - 2rE2 = - 2(r+R).(R + 2r).i + 2r².i + R.(r+R).i
r.E1 - 2rE2 = i.[- 2(r+R).(R + 2r) + 2r² + R.(r+R)]
r.E1 - 2rE2 = i.(-2rR - 4r² - 2R² - 4rR + 2r² + Rr + R²)
r.E1 - 2rE2 = i.(-5rR - 2r² - R²)
2rE2 - r.E1 = i.(5rR + 2r² + R²)
i = (2E2 - E1).r/(5rR + 2r² + R²)
-----
Calculs à vérifier bien entendu. 
Er cette méthode est loin d'être la seule pout trouver la solution.




