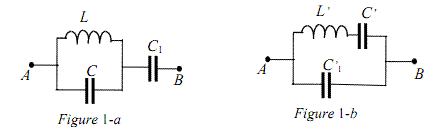Figure 1-a
----------
(C//L)+C1 ==> 1/z1=1/(jLw)+jcw =(1-LCw^2)/(jcw)==> z1=jcw/(1-LCw^2) ==> z=z1=jcw/(1-LCw^2)+jC1w
Même méthode pour les suivants

Distrait Barbidoux ?
Ton Z est quasi nul en très BF et presque infinie en HF ... Alors que c'est visiblement le contraire qu'on doit trouver.


1a)

L//C : 1/Z1 = jwC + 1/(jwL) = (1-w²LC)/jwL
z1 = jwL/(1-w²LC)

(L//C) série C1 : Z = z1 + 1/(jwC1)
Z = jwL/(1-w²LC) + 1/(jwC1)

Z = [-w²L.C1 + (1-w²LC)]/[jwC1.(1-w²LC)]

Z = (1-w²L(C+C1))/[jwC1.(1-w²LC)]

Z = -j.(1-w²L(C+C1))/[wC1.(1-w²LC)]
-----
Sauf distraction.  

Non mais copier-collé trop rapide et mauvaise relecture il fallait bien sur lire z=z1+1/(jC1w)=[i]jcw/(1-LCw^2)+1/(jC1w)
Merci d'avoir corrigé[/i]