Inscription / Connexion Nouveau Sujet
Prisme-Déviation et dispersion
Bonsoir,
J'ai un exercice d'optique géométrique et je ne vois pas comment le résoudre.
Enoncé:
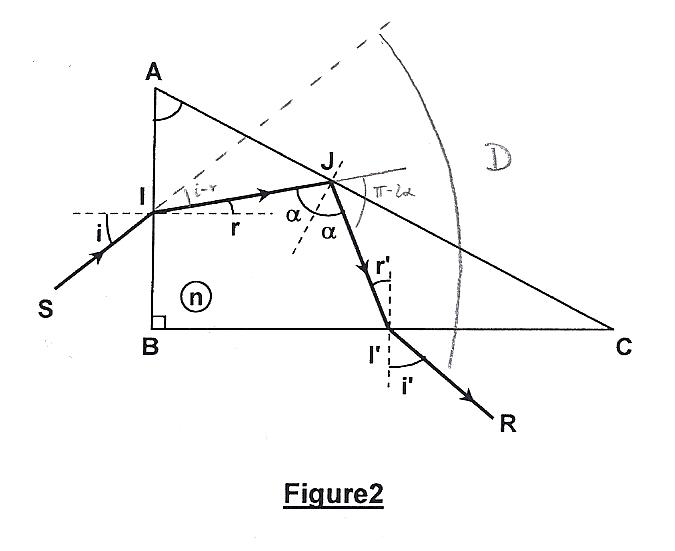
Un prisme de verre, d'indice n=1,6 pour la radiation jaune utilisée, a pour section droite un triangle rectangle ABC (Figure 2). Un rayon lumineux SI, situé dans le plan de section droite, pénètre par la face AB sous l'angle d'incidence , se réfléchit totalement sur l'hypoténuse AC et émerge à travers BCn on notera i' l'angle d'émergence.
-Calculer la déviation totale du rayon lumineux SI en fonction de i et i'.
J'ai D=(i-r)+( -2
-2 )-(i'-r')
)-(i'-r')
Si l'on peut utiliser Arcsin je sais exprimer r et r' en fonction de i mais je sais pas comment faire pour  -2
-2 .
.
-On donne A=60°. Pour quelle valeur de l'angle d'incidence i, le rayon émergent I'R est-il perpendiculaire au rayon incident SI ? En déduire les valeurs des angles de réfraction et de réflexion.
Merci d'avance pour l'aide.
Bonsoir Mac9,
ta figure a un gros avantage : elle est claire et m'epargne la peine d'en faire une autre ! Alors on reprend tes questions :
Calcul de la deviation D :
Ta as raison, en comptant > 0 les deviations qui font tourner le rayon dans le sens des aiguilles d'une montre (donc en I et en J) et < 0 dans l'autre sens (donc en I'), on obtient bien D = (i-r) + ( -2
-2 ) - (i'-r').
) - (i'-r').
Dans le triangle IAJ, on ecrit que la somme des trois angles vaut 2 , soit : (
, soit : ( /2-r) + A + (
/2-r) + A + ( /2-
/2- ) =
) =  , dont on tire r = A -
, dont on tire r = A -  .
.
Dans le triangle JCI', meme travail, soit ( /2-
/2- ) + C +
) + C +  /2+r') =
/2+r') =  , dont on tire r' =
, dont on tire r' =  - C. Or comme A + C =
- C. Or comme A + C =  /2, cette relation devient r' =
/2, cette relation devient r' =  + A -
+ A -  /2, soit avec l'expression de
/2, soit avec l'expression de  r' = 2A - r -
r' = 2A - r -  /2.
/2.
En reportant r, r' et  dans l'expression de la deviation D, tu obtiendras facilement D = i - i' +
dans l'expression de la deviation D, tu obtiendras facilement D = i - i' +  /2.
/2.
Des lors, la condition pour laquelle le rayon emergent I'R est perpendiculaire au rayon incident SI saute aux yeux : il faut que i' = i, soit r' = r. Cela donne A -  = A +
= A +  -
-  /2, ou encore
/2, ou encore  =
=  /4.
/4.
Il faut aussi s'assurer que le rayon subisse bien une reflexion totale en J, donc que  > il avec sin(il) = 1/n, n etant l'indice de refraction du prisme. Comme
> il avec sin(il) = 1/n, n etant l'indice de refraction du prisme. Comme  =
=  /4, on en tire n >
/4, on en tire n >  2.
2.
Avec r = A -  ou A et
ou A et  sont connus, tu peux facilement calculer l'angre L et en deduire celle de l'incidente particuliere i.
sont connus, tu peux facilement calculer l'angre L et en deduire celle de l'incidente particuliere i.
Est-ce OK ?
J'ai eu un petit pb d'ordi entre deux, mais mon post etait quasi termine.Dans la derniere phrase je voulais dire "r = A -  avec A =
avec A =  /6 et
/6 et  =
=  /4 te permet de calculer l'angle r et d'en deduire la valeur de l'incidence parcituliere i".
/4 te permet de calculer l'angle r et d'en deduire la valeur de l'incidence parcituliere i".
Bonne fin de week-end et a bientot, si tu as d'autres soucis avec l'optique.
Prbebo.
Merci pour cette réponse,
effectivement je trouve D = i - i' +  /2.
/2.
Par contre A= /3.
/3.
Pour r je trouve r= /12, ce qui fait que i
/12, ce qui fait que i 24,46°
24,46° 5
5 /37.
/37.
rebonsoir Mac9,
je m'apercois que j'ai oublie de repondre a ton dernier post concernant le prisme. Avec  =
=  /4, A =
/4, A =  /3 et r = A -
/3 et r = A -  on trouve facilement r = 15o, soit avec n =
on trouve facilement r = 15o, soit avec n =  2 (la valeur qui assure une reflexion totale en J dans le cas ou i = i'), on obtient i = 21.47o. Donc 21 au lieu de 24.
2 (la valeur qui assure une reflexion totale en J dans le cas ou i = i'), on obtient i = 21.47o. Donc 21 au lieu de 24.
A bientot, Prbebo.
S'il vous plait professeur prbebo pouvez vous m'expliquer comment vous trouvez la réponse de la dernière qustion parce que j'ai pas compris
Re - bonjour angelsirene,
Bonjour prbebo  si tu es de passage !
si tu es de passage !
angelsirene >> Pour la dernière question dont la méthode de résolution est donnée par prbebo dans son message du 02-10-11 à 21 h 28, je suis d'accord avec l'application numérique de Mac9. Pour n = 1,6 (donnée de l'énoncé) i  24,46°
24,46°

Bonjour Coll !
oui oui, je suis de passage, mais pour très peu de temps car je suis en vacances (dans la Creuse) et dois bientôt partir pour la balade journalière. J'aurai plus de temps cet après-midi pour relire les messages de angelsirene et y répondre. En attendant, si tu peux la prendre en charge ça me dépannerait. A tout à l'heure, B.B.
merci A vous mais j'ai pas parlé sur l'application numérique je veux comprendre la raison pour truver la condition pour laquelle le rayon emergent I'R est perpendiculaire au rayon incident SI ???
Il n'est guère possible d'expliquer mieux que prbebo dans son message du 02-10-11 à 21 h 28
Ce qu'il faut savoir :
. Les mots "perpendiculaire" ou "perpendiculairement" :  /2 rad
/2 rad
. Somme des angles d'un triangle :  rad
rad
. Un angle plat :  rad
rad

oui merci mais quelle methode tu as utilisé pour trouver i et tu sais juste angle A et la difference entre i et i' est π/2 ? S'il vous plait tu peux m'expliquer avec les détailles??
Bonjour Angelsirene, et bonjour Coll ,
Désolé pour mon silence dimanche, il y a eu une panne de réseau wifi à l’hôtel… ça marche maintenant, donc voici quelques explications pour Angelsirene :
1 – Pour le calcul de la déviation D, je ne peux rien ajouter à ce que j’ai déjà écrit dans ma première réponse à Mac9 : D = (i – r) + ( – 2
– 2 ) – (i’ – r’), soit en développant et en regroupant les termes D = i – i’ +
) – (i’ – r’), soit en développant et en regroupant les termes D = i – i’ +  – (r – r’ + 2
– (r – r’ + 2 ).
).
2 – La démonstration que j’ai donnée pour montrer que D = i – i’ +  /2 n’est pas la meilleure ; en voici une autre, plus simple :
/2 n’est pas la meilleure ; en voici une autre, plus simple :
Tu prends le quadrilatère BIJI’ : dans tout quadrilatère non croisé (c'est-à-dire pour lequel les côtés n’ont pas de points communs autres que leurs sommets), la somme des quatre angles fait quatre fois l’angle droit, soit 2 (facile à montrer : il suffit de tracer une diagonale pour partager le quadrilatère en deux triangles, dans chacun desquels la somme des angles vaut
(facile à montrer : il suffit de tracer une diagonale pour partager le quadrilatère en deux triangles, dans chacun desquels la somme des angles vaut  ).
).
Donc dans BIJI’ j’écris :  /2 + (
/2 + ( /2 + r) + 2
/2 + r) + 2 + (
+ ( /2- r’) = 2
/2- r’) = 2 , ce qui donne r – r’ + 2
, ce qui donne r – r’ + 2 =
=  /2. OK ?
/2. OK ?
Or on remarque que cette quantité se retrouve dans l’expression de D écrite ci-dessus : on en profite et on obtient D = i – i’ +  –
–  /2, soit D = i – i’ +
/2, soit D = i – i’ +  /2.
/2.
Dès lors, pour que D soit égale à  /2, il faut que i – i’ = 0 soit i’ = i.
/2, il faut que i – i’ = 0 soit i’ = i.
Angelsirene, il faut que tu comprennes que ce résultat n’a rien à voir avec l’optique géométrique, car il ne dépend pas de l’indice de réfraction du milieu ; il ne dépend pas non plus des angles A et C, donc de la forme de la section du prisme. Il faut juste que l’angle B soit un angle droit. Pour t’en convaincre, regarde la figure ci-dessous : deux droites sont perpendiculaires en B, on prend un point I sur l’une et un point I’ sur l’autre, et on trace en I et I’ deux droites (en bleu) inclinées du même angle i par rapport aux normales des deux premières : ces deux droites bleues forment bien un angle droit.
Revenons à l’exercice :
Les lois de Snell-Descartes en I et I’ s’écrivent :
En I : sini = n.sinr, et en I’ : sini’ = n sinr’ (dans le programme de physique de seconde, on voit plutôt n1.sini1 = n2.sini2, qu’on peut écrire plus simplement, par exemple en I en faisant n1 = 1 (vide), n2 = n (verre), i1 = i et i2 = r).
La condition précédente, i’ = i, impose donc l’égalité des angles r et r’.
Avec la relation r – r’ + 2 =
=  /2, on obtient alors 2
/2, on obtient alors 2 =
=  /2 soit
/2 soit  =
=  /4. Là encore, il ne s’agit pas d’un résultat issu de l’optique, mais d’une simple propriété géométrique : pour que i’ soit égal à i, il faut que l’angle IJI’ soit un angle droit.
/4. Là encore, il ne s’agit pas d’un résultat issu de l’optique, mais d’une simple propriété géométrique : pour que i’ soit égal à i, il faut que l’angle IJI’ soit un angle droit.
Tu es toujours là ? Si oui, alors l’exercice est quasiment fini : il ne reste plus qu’à calculer les angles i et r en utilisant les données de l’énoncé, soit A = 60° et n = 1,6. Pour cela, on a besoin d’une relation liant l’angle r à l’angle A, qu’on obtient par exemple en écrivant que dans le triangle AIJ la somme des angles vaut  . Voir ma réponse à Mac9 (02/10/11, 21h28) : on obtient facilement r = A –
. Voir ma réponse à Mac9 (02/10/11, 21h28) : on obtient facilement r = A –  . Avec A = 60° et alp = 45° (
. Avec A = 60° et alp = 45° ( /4…), on obtient r = 15°.
/4…), on obtient r = 15°.
La loi de Descartes en I donne alors sini = 1,6 x sin(15°) = 0,414, soit i = 24,46°.
Les réponses demandées sont donc : i = i’ = 24,46° , r = r’ = 15°,  = 45°.
= 45°.
Pour Coll : en effet j’ai zappé l’info concernant l’indice de réfraction du prisme, cad 1,6. Pour Mac9 j’ai juste montré que pour qu’il y toujours réflexion totale en J il faut que n soit supérieur à  2 et j’ai fait le calcul de angles avec cette valeur…
2 et j’ai fait le calcul de angles avec cette valeur…
Pour Angelsirene, qui es nouvellement inscrit(e) sur le forum, voici deux petites remarques qui n’ont rien d’acerbe et qui t’aideront à rester en bons termes avec les correcteurs du forum :
- quand on requiert une aide pour résoudre un exercice, une formule de politesse (un simple bonjour par exemple) est toujours la bienvenue ;
- lorsqu’on pose une question un samedi du mois d’août (donc en pleines vacances ici) et à 20h40, il ne faut pas s’étonner qu’à 20h43 la réponse ne soit pas encore venue. Il faut savoir être patient…
Si tu as d’autres soucis avec cet exercice, n’hésite pas à les poser, Coll et moi sommes là pour ça.
Bonne journée, prbebo.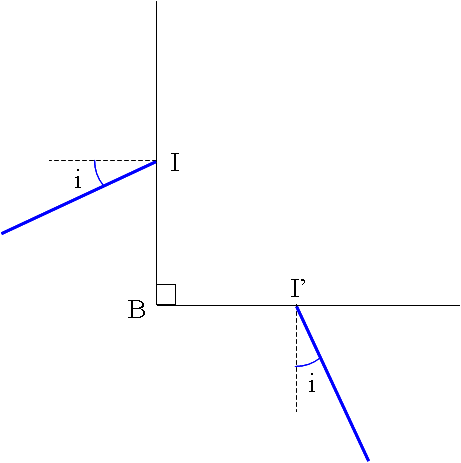
Bonjour prbebo 
J'avais bien compris pour n = 1,6 et pour n 
 2. Quand on reprend une aide, on ne relit pas toujours tout le topic. Je m'étais permis le message du 03-08-14 à 7 h 54 pour le cas où les questions de 20 h 40 et 20 h 43 ( !
2. Quand on reprend une aide, on ne relit pas toujours tout le topic. Je m'étais permis le message du 03-08-14 à 7 h 54 pour le cas où les questions de 20 h 40 et 20 h 43 ( !  ) auraient eu cette valeur de l'indice pour origine. Mais il me semble que angelsirene est loin de cela.
) auraient eu cette valeur de l'indice pour origine. Mais il me semble que angelsirene est loin de cela.
Je pense qu'un énoncé bien construit aurait dû demander aux élèves (s'ils ne sont pas assez formés pour le faire d'eux-mêmes...) de vérifier qu'il y a bien réflexion totale sur AC.
Et si maintenant angelsirene ne comprend pas, c'est à désespérer...