Inscription / Connexion Nouveau Sujet
Principe d'un déversoir / Hydrostatique
Bonjour tout le monde,
Je travaille sur un exercice qui concerne le débit volumique principalement et j'ai un peu du mal, j'ai fais ce que j'ai pu et je demande votre aide !!
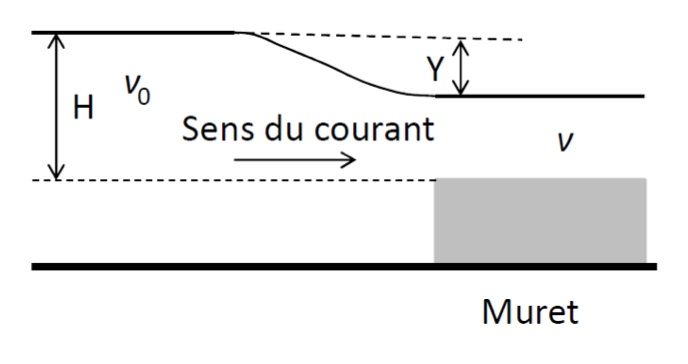
La vitesse de l'eau dans le canal est v0 : elle est uniforme. La surface de l'eau est à une hauteur H au-dessus du niveau correspondant au sommet du muret. Au moment du passage au-dessus du muret, la surface de l'eau perd une altitude Y par rapport à l'amont. Le seuil du réservoir est assez large pour que les filets d'eau au-dessus de lui puissent être considérés comme horizontaux. On suppose que l'écoulement parfait est stationnaire, le fluide est incompressible. Le canal est horizontal, à section rectangulaire de largeur L. On appelle  la masse volumique de l'eau et g l'accélération de pesanteur.
la masse volumique de l'eau et g l'accélération de pesanteur.
1) On suppose que la vitesse du fluide v est uniforme au-dessus du muret. Déterminer le débit volumique D à l'endroit du déversoir en fonction de v, H, Y et L.
=> On trouve le débit volumique par la relation :
Qv= S1*v1=S2*v2
Dans notre cas, on peut écrire : D =  *L*(H-Y)*v
*L*(H-Y)*v
(j'ai utilisé la formule de l'aire d'un cylindre)
2) Déterminer la pression P au sommet du muret en fonction de P0 pression atmosphérique, Y, H,  et g.
et g.
=> J'utilise : P(z) = P0- *g*z
*g*z
(j'ai trouvé cette relation dans un exercice et je voulais savoir si on peut l'écrire directement ?)
donc on a: P(H)= P0 - *g*(H-Y)
*g*(H-Y)
3) En prenant un point à la surface de l'eau en amont et un autre à la surface de l'eau au-dessus du muret, appliquer le théorème de Bernouilli. En déduire une relation entre v0, v et les donnés du problème.
=> Le théorème de Bernouilli est : 1/2 *v1^2+ P1+
*v1^2+ P1+  gz1 = 1/2
gz1 = 1/2 *v2^2+ P2+
*v2^2+ P2+  gz2
gz2
donc : 1/2 *v0^2+ P0+
*v0^2+ P0+  gH = 1/2
gH = 1/2 *v^2+ P+
*v^2+ P+  g(H-Y)
g(H-Y)
(Je sais pas du tout si c'est comme ça qu'il faut faire !)
4) Exprimer D en fonction de v0, H, Y et L
Cette question me semble la même que la 1) mais je pense qu'il faut juste prendre un point qui est en amont du muret d'où:
D=  *L*H*v0
*L*H*v0
5) Le débit est stationnaire lorsque qu'il est maximal au-dessus du muret. On l'appelle alors Dmax. Si on suppose que la vitesse v0 est quasiment nulle en amont du muret, pour quelle valeur "Y" a-t-on un débit maximal ? En déduire l'expression Dmax en fonction de H, g et L.
=> A partir de cette question je suis perdue ...
Je pense que plus Y est grand et plus on a un débit maximal mais je ne sais pas quelle valeur on doit prendre ... Et du coup je n'ai pas d'idées pour la relation de Dmax 
6) On suppose à présent que v0 est nulle. A l'aide d'une tige graduée plongée dans le canal en différents endroits, il est possible de mesurer H, Y ainsi que la hauteur du muret h.
Justifier et écrire la conservation du débit avant le muret et au-dessus du muret. En déduire qu'il est possible de déterminer v0 en se servant de ces mesures. Déterminer la relation entre v0, H, Y et h.
=> Pareil pour cette question on me demande d'écrire la relation de D mais à part la relation que j'ai marquée dans la première question je ne sais pas comment en déduire une autre.
Mon exercice est assez long mais j'aimerais vraiment avoir vos avis s'il vous plait !!
bonsoir,
1) la section est rectangulaire donc: D = L(H-Y)v
2) la pression statique en haut du muret vaut: Po + g(H-Y)
g(H-Y)
3) on peut appliquer effectivement le théorème de Bernouilli:
1/2*v0^2+ P0 + gH = 1/2*v^2+ P0 + g(H-Y)
ce qui donne: v2 = v02 +2gY
4) on en déduit D = L(H-Y)v = L(H-Y) (v02 +2gY)
(v02 +2gY)
5) D = f(Y)  L(H-Y)
L(H-Y) 2gY si on néglige Vo2 devant 2gY
2gY si on néglige Vo2 devant 2gY
on cherche le maximum de f(Y) càd Y tel que f'(Y)=0
6) question curieuse
en amont: D = (H+h)LVo
or D  L(H-Y)
L(H-Y) 2gY si on néglige Vo2 devant 2gY
2gY si on néglige Vo2 devant 2gY
d'où (H+h)LVo  L(H-Y)
L(H-Y) 2gY
2gY
Vo  ...
...
sauf erreur