Inscription / Connexion Nouveau Sujet
Pression d'une demi-sphère
Bonjour,
Je bloque sur la question suivante qui a pourtant l'air tout bête...
Merci d'avance pour votre aide ! 
____________________________________________________________________________________________________________
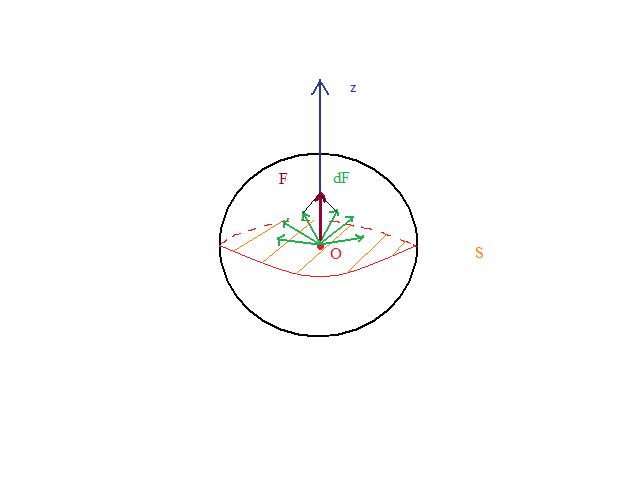
Montrer que la force de pression exercée sur une demi-sphère de rayon par une pression uniforme
est donnée par
. On donne
en coordonnées sphériques.
____________________________________________________________________________________________________________
Je suis parti de .
Donc en sommant on arrive à .
D'où vient mon erreur ?
Merci bien  .
.
Bonjour, il y a une erreur dans la formule que tu proposes.
L'aire d'une sphère est 4 r2 donc pour une demi-sphère on a 2
r2 donc pour une demi-sphère on a 2 r2.
r2.
Po = F/S -> F = Po.S = Po 2 r2
r2
Il faut ensuite intégrer de 0 à  /2 et tu balaies toute la sphère
/2 et tu balaies toute la sphère 
Rectification : de 0 à  tu balaies toute la sphère (d'où 4Po
tu balaies toute la sphère (d'où 4Po r2 en résultat).
r2 en résultat).
En revanche, de O à  /2 c'est la demi-sphère que tu balaies
/2 c'est la demi-sphère que tu balaies 
Merci gbm mais j'avais bien utilisé "" et non 4.
Par contre pourquoi faut-il aller de à
et non de
à
? Sur la figure, on voit que l'angle
peut varier de
à
...
Et avec votre calcul j'obtiens alors que le résultat devrait être
.
Il y a donc toujours un problème ! ...
Le problème est le suivant :
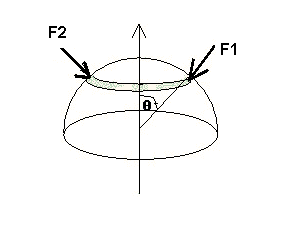
La force est répartie sur toute la demi sphère.
Considérons 2 forces (sur deux éléments de surfaces) resultant de la pression comme se les ai dessinées
Il est évident que si on cherche la résultante de ces 2 forces, seule subsite une composante parallèle à l'axe, les composantes perpendiculaires à l'axe de F1 et F2 se compensent.
Et c'est pareil pour toute force élementaire sur n'importe quel morceau de demi sphère, il existe une autre force élémentaire qui compense la composante de la force perpendiculaire à l'axe.
Donc il pour calculer la force résultante (pas confondre avec l'écrasement), il ne faut considérer que la composante des forces de pression parallèle à l'axe (donc ici verticale sur le dessin)
Et on peut se taper une intégrale (de la composante verticale de la pression.dS sur la demi sphère) ou réfléchir que cela revient à multiplier la pression Po par l'aire de la sphère vue par un observateur qui se trouverai très loin dans la direction de l'axe.
Cette aire est celle du cercle de base de la demi-sphère, soit S = Pi.R² (à ne pas confondre avec l'aire de la demi-sphère).
Et donc la force résultante (celle qu'il faudrait faire pour soulever la demi sphère avec la pression Po à extérieur et le vide sous la demi sphère (Poids de la matière négligé) est donc: F = Po.S = Pi.R².Po
-----
Sauf distraction. 
Merci beaucoup pour votre réponse J-P, il est vrai que le raisonnement est intéressant et se comprend bien mais l'énoncé incite à calculer une intégrale vue les données fournies.
C'est pourquoi je voudrais savoir comment calculer cette intégrale CORRECTEMENT parce que MON raisonnement est FAUX quelque part puis je n'aboutis pas à l'expression de la force attendue...
Merci d'avance pour vos éclaircissements !
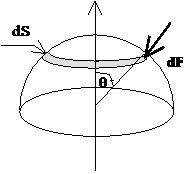
La composante verticale (// à l'axe) de la pression est Po.cos(theta) -->
dF = Po.cos(theta). 2Pi.r².sin(theta) d theta
dF = Pi.r² Po. sin(2.theta) d theta
F = Po. Pi.r²/2 . [-cos(2.theta)](de 0 à Pi)
F = P0 . Pi.r²/2 * 2
F = Po. Pi.r²
-----
Sauf distraction. )
Salut J-P, une chose où au moins j'avais raison 
En revanche, dans le cas d'une pression uniformément répartie sur la demi-sphère. Ma formule marche bien ou non ? Merci (au moins j'apprendrai en même tps quelque chose)
De 0 à pi/2 mais auriez-vous une explication à cela ?
J'avoue que ce n'est pas très clair pour moi...
Merci !
Si tu regarde ton schéma, l'angle varie entre 0 et Pi/2. Cela suffit pour couvrir toute la demi-sphère.
Salut gbm,
La pression est bien considérée la même partout sur la demi sphère dans mon raisonnement.
Comme je l'ai expliqué, pour chaque élément de surface, la force sur cet élément de surface résultant de la pression peut se décomposer en une composante verticale et une composante horizontale.
Et si on considère maintenant l'élement de surface (de même taille) symétrique par rapport à l'axe dessiné, la force due à la pression sur cet autre élément de surface peut aussi se décomposer en une composante verticale et une composante horizontale.
Les composantes horizontales (perpendiulaires à l'axe) des forces sur les 2 éléments de surface ci-dessus sont de même norme, même direction, mais de sens opposés.
Et donc ces composantes horizontales des forces se compensent.
Ceci est vrai pour tout élément de surface de la demi sphère, il y a toujours un élément de surface de la demi sphère symétrique par rapport à l'axe qui fait que les composantes des forces dues à la pression perpendiculaire à l'axe se compensent (et donc se neutralisent)
Donc si on veut calculer la force qu'il faudrait faire pour soulever la demi sphère avec la pression Po à extérieur et le vide sous la demi sphère (Poids de la matière négligé), on ne doit considérer que les composantes verticales (// à l'axe de la demi sphère) des forces dues à la pression.
Et pour chaque élément de surface dS de la demi sphère, la composante verticale de la force due à la pression est dF = Po.cos(theta).dS
En intégrant cela sur theta de 0 à Pi/2, on trouve F = Po. Pi.r²
Ce résultat est bien celui du à une pression Po uniforme partout sur la demi sphère.
-----
Attention, le fait que les composantes perpendiculaires à l'axe de la demi sphère se compensent ne signifie pas qu'elles ne jouent aucun rôle dans aucun cas, mais seulement qu'elles n'influencent pas la force à faire pour soulever la demi-sphère.
Dans le même ordre d'idée :
Si on avait une sphère pleine, faire le vide dedans (à part le poids de l'air) n'influence pas la force qu'il faut faire pour soulever la sphère mais il n'empêche que la sphère pourrait bien s'écraser.
Donc, il faut savoir ce qu'on cherche, la force due à la pression qu'il faut vaincre si on veut soulever le bidule ou bien la "force d'écrasement" due à la pression, mais cette dernière n'est pas vraiment une force telle qu'on l'entend en physique, on ne peut en effet pas lui donner une direction, ni un sens, puisque ceux-ci sont différents sur chaque élément de surface et que si on fait la somme vectorielles des forces élémentaires sur toute la surface (cas de la sphère complète) on trouvera 0.
-----
J'espère que ces commentaires ne t'embrouilleront pas plus encore.


Ok merci pour cette explication. Je m'embrouille dans la mesure où je ne vois pas la différence entre cet exercice et une partie d'un concours :
Banque PT 2000 (extrait de SI B) : Banc d'essai de rotules de prothèses fémorales
_____________________________
Il s'agit d'un sujet de conception qui étudie une machine qui teste l'usure des têtes de prothèses fémorales. Dans une question, il est dit que (désolé je n'ai pas réussi à trouver un lien vers le sujet) :
- Action de la coupelle sur la sphère -
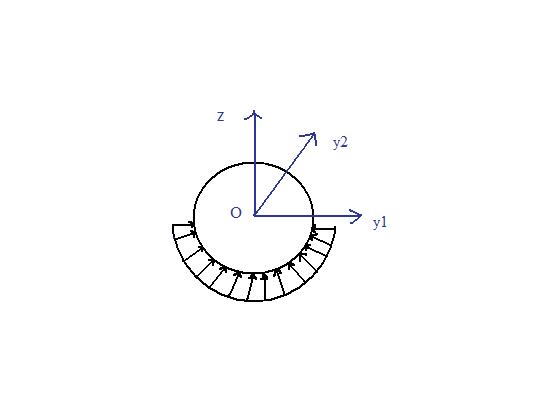
La détermination des actions sur les roulements constituant le guidage de l'arbre secondaire passe par la connaissance de l'action de la coupelle sur la sphère. Le système de mise en charge à l'aide de rondelles ressorts génère un effort de la coupelle sur la sphère (F = 2500 N appliqué en O suivant l'axe z).
On considère que le contact sphère sur coupelle s'établit sans jeu sur une demi-sphère (de rayon R=17,5 mm) avec une répartition de pression uniforme P (voir schéma ci-dessous).
Déterminer l'expression de la pression radiale de contact en fonction de F et R.
_____________________________
Lors de la correction, le professeur de sciences industrielles nous a dit que F = P*2 R2. Voilà le problème
R2. Voilà le problème 
Si j'ai bien interprété l'énoncé, oui il s'est trompé.
Raisonnement par l'absurde.
La sphère est à l'équilibre et donc la somme vectorielle des forces appliquées à la sphère est nulle.
Supposons que la sphère est remplacée par une surface horizontale de même aire qu'une demi sphère (soit 2Pi.R²) et avec une pression P sous le plan uniquement.
Dans un tel cas, avec F = P*2Pi.R² la surface plane est bien en équilibre.
Mais on remarque que toutes les forces élémentaires dF1 sur le "fond" du plan sont verticales vers le haut (due à la pression P), elles sont de même direction et de même sens (verticale, vers le haut) et suffisent juste à maintenir la charge P (et donc la surface plane est à l'équilibre). (F vertical vers le bas juste compensé par la pression P sur une aire P*2Pi.R² telle que F = P*2Pi.R²)
Si en gardant la même pression P, on incurve la surface plane en conservant son aire (pour la transformer en demi sphère), les forces dF1 ont la même norme qu'avant (qu'avec le plan), mais elles n'ont plus toutes la même direction (car elles sont normales aux élémentx de surface sphérique) et donc leur somme vectorielle diminue (elles n'on plus toutes la même direction) et donc la sphère ne peut pas être en équilibre.
Ceci montre que la pression ne peut pas être celle tirée de F = P*2Pi.R²
Cette pression doit augmenter.
...Et le calcul du début montre que P doit être tel que F = P*Pi.R².
Toujours si j'interpète bien l'énoncé avec la prothèse, mais je pense que oui.