Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

précision sur l'équation d'une onde plane

Posté par
vovik 16-01-18 à 23:18

Bonjour,

l'équation générale d'une onde plane est la suivante:
\vec{E}(\vec{r},t)=A\cdot cos(\omega t-2\pi \cdot \vec{k}\cdot \vec{r}+\varphi )

le vecteur r est le vecteur de position: \vec{r}=(x_{r},y_{r},z_{r})
le vecteur k c'est quoi son rôle?
si le vecteur k est de coordonnées \vec{k}=(a,b,c)
alors le produit donne \vec{k}\cdot \vec{r}=a\cdot x_{r}+b\cdot y_{r}+c\cdot z_{r}=> \left \| \vec{k}\cdot \vec{r} \right \|=\sqrt{(a\cdot x_{r})^2+(b\cdot y_{r})^2+(c\cdot z_{r})^2}
pourquoi le produit scalaire de ces 2 vecteurs? quelle sont les questions générales dans lesquelles il faut exploiter ce produit scalaire?

Cordialement.

Posté par
vanoisere : précision sur l'équation d'une onde plane 16-01-18 à 23:50

Bonsoir
Le vecteur d'onde \overrightarrow{k} est un vecteur ayant pour direction, la direction de propagation, pour sens le sens de propagation et pour norme : k=\frac{2\pi}{\lambda}=\frac{\omega}{c}.

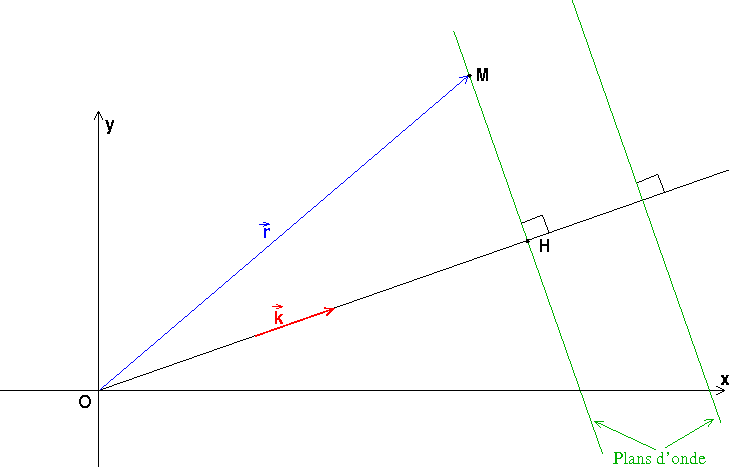
Par définition d'une onde plane, tous les points M(xr,yr,zr) de l'espace appartenant à un même plan (appelé plan d'onde) perpendiculaire à la direction de propagation (donc perpendiculaire à \overrightarrow{k} ) vibrent en phase. Soit O l'origine du repère et H l'intersection du plan d'onde avec la droite passant par O et dirigée par \overrightarrow{k} . Propriété du produit scalaire : pour tout point M du plan d'onde :

OH=\frac{\overrightarrow{k}}{k}.\overrightarrow{r}

Soit \vec{E}(O,t)=A\cdot cos(\omega t+\varphi) le vecteur champ en O à la date t. En absence d'amortissement, le point H reproduit le signal en O avec un retard \left(\frac{OH}{c}\right). Le vecteur champ en H à la date t est donc celui existant en O à la date \left(t-\frac{OH}{c}\right). D'où l'expression du vecteur champ en H et donc aussi du vecteur champ en M puisque M et H appartiennent au même plan d'onde :

\vec{E}(\overrightarrow{r},t)=A\cdot cos(\omega\left(t-\frac{OH}{c}\right)+\varphi)=A.\cos\left(\omega.t-\omega\frac{\overrightarrow{k}.\overrightarrow{r}}{k.c}+\varphi\right)=A.\cos\left(\omega.t-\overrightarrow{k}.\overrightarrow{r}+\varphi\right)

puisque k.c=\omega

Fait un schéma si cela ne te parait pas clair.

Posté par
vanoisere : précision sur l'équation d'une onde plane 17-01-18 à 12:09

Voici un schéma ; il est en 2D mais il pourra sans doute t'aider quand même !

précision sur l\'équation d\'une onde plane

Posté par
vovikre : précision sur l'équation d'une onde plane 17-01-18 à 13:33

Bonjour,
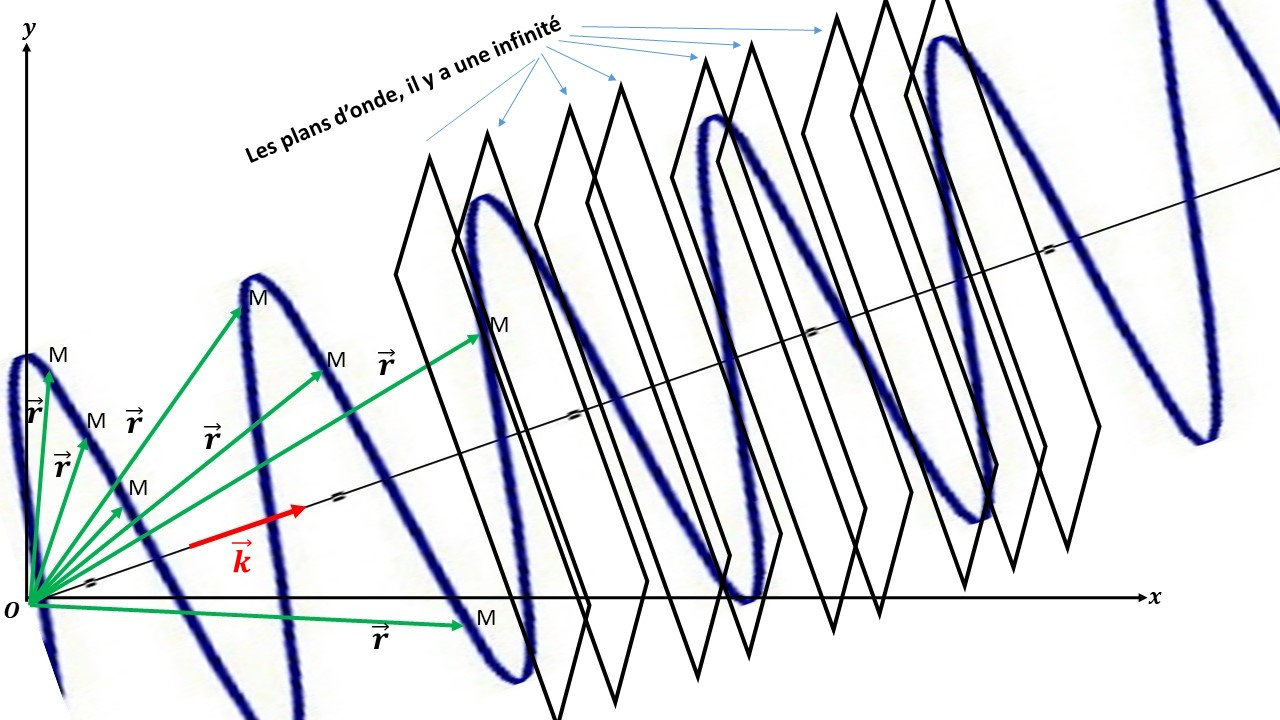
pour renforcer mon interprétation graphique d'une onde et de vecteurs qu'on utilise, pourriez-vous me dire si cette image est juste?
précision sur l\'équation d\'une onde plane

Merci d'avance,
Cordialement

Posté par
vanoisere : précision sur l'équation d'une onde plane 17-01-18 à 13:48

Bravo pour tes représentations de plans d'onde en 3D ! Il y a effectivement une infinité de plans d'ondes tous parallèles entre eux.
A un instant t donné,  chaque coordonnée non nulle du vecteur E est effectivement une fonction sinusoïdale de la distance OH , la distance entre deux maximums consécutifs étant égale à . Donc, à un instant donné quelconque, le vecteur E est le même en tous les points d'un plan d'onde donné (P) mais il est aussi le même en tous les points des plans d'onde distants de (P) d'un multiple de la longueur d'onde.
Remarque à propos des notations : A représente un vecteur, il serait plus correct de noter :

\vec{E}(\vec{r},t)=\vec{A}\cdot cos(\omega t-  \vec{k}\cdot \vec{r}+\varphi )
J'espère que tu avais bien remarqué l'absence du "2" dans l'expression de la phase, contrairement à ce que tu as écris dans ton premier message.

Posté par
vovikre : précision sur l'équation d'une onde plane 17-01-18 à 16:11

Rebonjour,

supposons cette équation d'onde:

\left\{\begin{matrix} E_{x}=\frac{1}{\sqrt{2}}\cdot E_{0}\cdot e^{j[2\pi 10^{10}t-\frac{2\pi40}{\sqrt{2}}(x+y)]}\\ E_{y}=-\frac{1}{\sqrt{2}}\cdot E_{0}\cdot e^{j[2\pi 10^{10}t-\frac{2\pi40}{\sqrt{2}}(x+y)]}\\ E_{z}=0 \end{matrix}\right.

puisque la forme générale s'écrit aussi: \vec{A}\cdot cos(\omega t-\vec{k}\cdot \vec{r}+\varphi )

supposons que le vecteur \vec{k} est de coordonnées: \vec{k}=\begin{pmatrix} a\\ b\\ c \end{pmatrix}
et que le vecteur de position \vec{r} est de coordonnées: \vec{r}=\begin{pmatrix} x_{r}\\ y_{r}\\ z_{r} \end{pmatrix}

alors \vec{k}\cdot \vec{r}=a\cdot x_{r}+b\cdot y_{r}+c\cdot z_{r}=\frac{2\pi40}{\sqrt{2}}x+\frac{2\pi40}{\sqrt{2}}y=> a=\frac{2\pi40}{\sqrt{2}}\; et\; b=\frac{2\pi40}{\sqrt{2}}\; \;
et donc le vecteur directeur d'onde est de coordonnées: \vec{k}=\begin{pmatrix} \frac{2\pi40}{\sqrt{2}}\\ \frac{2\pi40}{\sqrt{2}}\\ 0 \end{pmatrix}

Est'ce juste?

En effet ces questions me permettent de bien comprendre ce qui se passe au niveau des vecteurs.

Cordialement.

Posté par
vovikre : précision sur l'équation d'une onde plane 17-01-18 à 16:21

Le vecteur k n'était censé être un vecteur unitaire?

Posté par
vanoisere : précision sur l'équation d'une onde plane 17-01-18 à 16:41

Pour vérifier la cohérence de ce que tu as fait, j'ai commencé par déterminer la célérité de cette onde. Sa fréquence est f=1010Hz ; sa longueur d'onde est :

\lambda=\frac{2\pi}{k}=2,5.10^{-2}m\quad puisque\quad k=\left(80\pi\right)m^{-1}
La célérité de l'onde est :

V=\lambda.f=2,5.10^{8}m/s
Ce résultat est acceptable pour une onde électromagnétique. Une valeur supérieure à la vitesse de la lumière dans le vide aurait évidemment été incohérente.
Tu dois aussi savoir qu'une onde électromagnétique plane est une onde transversale : le vecteur champ E est à chaque instant orthogonal à la direction de propagation :

\overrightarrow{E}\cdot\overrightarrow{k}=0\;\forall t ; ce qui est le cas.

Ce que tu as fait est donc tout à fait correct. Evidemment, si on te laisse le choix du repère, tu as tout intérêt à travailler dans un repère déduit du précédent par une rotation de \left(\frac{\pi}{4}\right)rad de façon à obtenir un vecteur k ayant une seule composante non nulle. L'expression du vecteur E est alors grandement simplifiée.

Posté par
vanoisere : précision sur l'équation d'une onde plane 17-01-18 à 16:46

Citation :
Le vecteur k n'était censé être un vecteur unitaire?

Bin sur que non ! Comme déjà expliqué :

k=\frac{2\pi}{\lambda}=\frac{\omega}{c}

D'où la nécessité, dans ma démonstration de hier soir nécessitant un vecteur unitaire dirigeant la droite OH, de faire intervenir le vecteur : \frac{\overrightarrow{k}}{k}

Posté par
vovikre : précision sur l'équation d'une onde plane 17-01-18 à 21:14

Bonjour,
Comment avez-vous trouvé la valeur du k=80pi?,
J'ai du faire le produit scalaire pour trouver cette valeur, y a t'il une méthode plus rapide? , l'extraire juste en visualisant l'équation?
Merci,
Cordialement.

Posté par
vanoisere : précision sur l'équation d'une onde plane 18-01-18 à 11:48

J'ai utilisé tes résultats puis posé tout simplement :

k=\Vert\overrightarrow{k}\Vert=\sqrt{a^{2}+b^{2}+c^{2}}

Posté par
vovikre : précision sur l'équation d'une onde plane 18-01-18 à 20:34

Merci Vanoise,

très utile pour moi.

Cordialement.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !