y=0 si. x= 0 yo=0
Y=0 si x=L/2 , y'0=17PL³ /384.E.I
Donc y=-p.x/384.E.I[96.xL² -64x² .L +16.x³ -17.L³ ]
C est ce que trouve finalement sur le troncon CD.
Aussi essaies de jeter un coup d oeil sur les conditions aux limites pour moi.merci de repondre .cordialement.

Je n avais pas ajoute la valeur de la constante dans le premier calcul.maintenant c est ce que je trouve.

Bjr Gbm.j ai de serieux probleme avec cet exercice.
Avec les valeurs des moments donnes, quand je trace le diagrammes des moments, je ne trouve pas ca conforme a la figure.merci

L1=l2=5 m
L=20 m

Quand je trace le diagramme avec les moments , seul le moment sur le troncon AB n est pas conforme.
Je trace sur CD et la moitie de AB et j en deduis l autre cote par symetrie.

Si y(x) est le déplacement de la poutre pour une abscisse x, on utilise généralement pour un appui :
y(l1) = 0
y(l1+l) = 0

--> pas de déplacement au niveau de l'appui.

équation de continuité :
y'(l1+) = y'(l1-), idem pour l'autre appui.

Peux-tu me poster les diagrammes de l'effort tranchant et moments fléchissant que tu trouves ?

Bjr Gbm.
La methode que tu propose est generalement utilise pour etudie la variation de l effort tranchant et du moment flechissant sur les differents troncons.c est juste comme methode mais je pense que ce n est pas ce qu on nous demande .on demande plutot d ecrire l equation de la ligne elastique ou on cherche a exprimer le deplacement en fonction de la charge appliquee , de l abscisse , de E et du moment d inertie sur chaque troncon.
J ai bien verifie tes reactions et tes efforts tout est correcte , vraiment correcte.
Mais dans l application pour le trace du diagramme des moments flechissants , j ai du mal a tracer sur l axe AB.pourtant I'll doot etre symetrique par rapport au troncon CD.

Je reconnais que les efforts que tu fournis pour moi m ammene de jour en jour a comprendre la RDM.en cas merci professeur.
Je t envoie le diagramme en mi journee.merci

On demande l equation de la ligne elastique en 0 milieu de l soit en l/2.
Tu vois un peu

Justement, les conditions aux limites peuvent te permettre de trouver les constantes d'intégrations que tu as quand tu intègres à deux reprises l'équation EIy"=Mfz pour chaque tronçon. Car sinon comment les trouves-tu ?

C'est que je m'évertue à te demander depuis 2j sans réponse claire de ta part .

Ok, j'attends tes tracés.

A+

Bjr Gbm, voici les conditions aux limites:
0xl1^-1
M(x)=-p.x² /2 et
Ty(x)=-p.x
X=l1^-1 M(l1^- )= -p.l1² /2
Et Ty=-p.l1
x=l1⁺
M= -p.l1² /2 et Ty= ?

Aussi
l1 x l1 + l2/2
M=?
Ty=?
Et le reste on en deduit par symetrie.ce que je cherche depuis voila pkoi je ne t ai pas repondu.I'll faudrait que je donne qd meme des reponses raisonnables meme si je cherche a comprendre.merci de repondre.

Voici le diagramme des moments.



** image supprimée **

Bjr .I'll faut essayer de recadrer l image pour moi merci.

Et l'effort tranchant ?

?

Bjr Gbm, cela fait des jours que je n arrive pas a definir les conditions aux limites de mon exo.
Je demande si tu as une proposition.
Au milieu de la portee , je define l equation differentielle
Y".EI=M(x) , j intingre ensuite pour trouver la valeur y.
Ensuite , je deduis la fleche a l abscisse x=L/2 avec L=l1 +l2+l.
Aussi sur les consoles ,
Je fais la meme methode mais en prenant pour valeur respectifs des abscisses l1 et l2.
Pour trouver les fleches correspondantes.mon problemes c est comment choisir les conditions aux limites afin de trouver les equations elastiques sur les differents troncons.merci de repondre.cordialement.

Bonjour siamni,

Je te les ai défini plus haut, c'est juste que tu ne prends pas le temps de lire ce que je t'ai proposé.

Ces conditions aux limites se trouvent au niveau des appuis B et C :
* déplacement nul en ce point ;
* continuité du déplacement pour les tronçons à gauche et à droite de chaque appui.

Avant tout chose, pour que tu puisses progresser, je t'ai demandé de me tracer les diagrammes Ty et Mfz pour m'assurer que tu as compris ce qu'on a pu déterminer par la calcul pour les tronçons AB, BC et CD (calculs pour lesquels tu m'as dit que tu avait compris les expressions que j'avais trouvées).

Objectifs :
-->vérifier si tu sais représenter graphiquement ce qui a été trouvé par le calcul ;
--> voir les conditions aux limites usuelles (ou non) ;
--> mieux appréhender visuellement la relation ô combien utile de dMfz/dx = -Ty.

Ensuite tu en viendras aux équations de déplacement EIy" = Mfz pour lesquelles tu pourras utiliser les conditions aux limites aux appuis telles que définies plus haut.

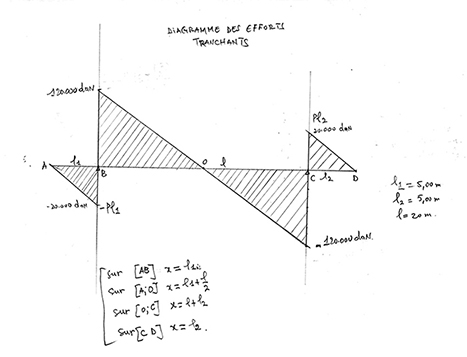
bonjour gbm ,voici le diagramme que je trouve.

a gauche de B ,
On a :
Ty=p.x
Mfz=-p.x² /2
continuite pour x= l1
Ty=p.l1
Mfz=-pl1²/2
A droite de B ,
on a :
Continuite pour x =l1 + l
Mfz=-pl2²/2
tu m avais deja dis ca .
est ce que cela peut me permettre de trouver les equation en question du moment ou on remplace les x par leur valeurs,
c est que je ne comprend pas.

voici le diagramme des efforts tranchants que je trouve, Gbm

Bonjour siamni,

Tu y es presque ! C'est bien!
Ton effort tranchant a la bonne allure ... Au signe près.

En effet, si je regarde à droit de C, la charge répartie est dans le sens opposé de l'axe Oy, donc le signe devrait être négatif.

Ensuite, l'effort en C créé une discontinuité qui le rend positif, etc.

Corrige ton diagramme. Et que remarques-tu entre l'évolution de Ty et Mfz ?

Bjr Gbm, j ai corrige mon diagramme comme tu me l.as conseille.je remarque que a Ty =0,
Mfz a un maximum a l abscisse x=(l1+l2+l)/2
Cependant avec l expression du .moment sur le.troncon BC , je trouve EI.Y"=Mfz
Pour l equation de la ligne elastique.
Mais je trouve la fleche :
Y=-pl2.(l1+l2+l)³ /32.EI
Aussi comment faire pour en deduire les fleches sur les consoles AB et BC .
Essaies de calculer pour la fleche sur la travee pour voir si je ne me suis pas tromper.merci de repondre .cordialement.

AB et CD .autant pour moi

Yo,

1. Diagramme sur un cas simple

Rappel des équations trouvées (non simplifiées) :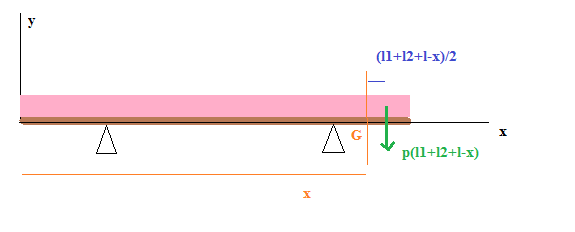



Soit une abscisse x entre C et D, le torseur de cohésion en G s'écrit (en faisant le bilan des efforts à droite de G) :

Ty = -p.(l1+l2+l-x) --> j'utilise le principe de saint-venant en me ramenant à un effort concentré au milieu de la portion à droite de G.
La longueur de cette portion est .

Mfz = -p.(l1+l2+l-x)²/2

--> bras de levier x effort dans le sens indirect du repère (d'où le signe moins)
--> l'effort est toujours le même pour cette portion, le bras de levier étant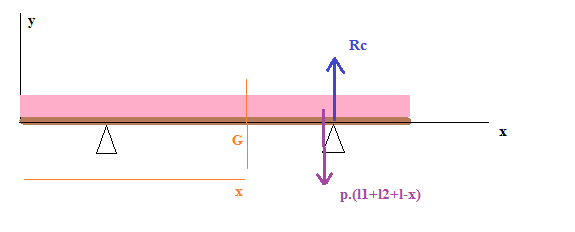



Ty = -p.(l1+l2+l-x) + Rc --> même effort concentré que précédemment + appui Rc si je regarde à droite de G
Ty = -p.(l1+l2+l-x) + 1/2.p.(l+l1+l2) --> en reprenant l'expression de Rc trouvée plus haut
Ty = -1/2.p.(l+l1+l2) + p.x --> en simplifiant, sauf erreur

Mfz = -p.(l1+l2+l-x)²/2 + (l1+l-x).Rc ---> même méthode que précédemment, effort x bras de levier, le signe dépendant du sens du repère
Mfz = -p.(l1+l2+l-x)²/2 + (l1+l-x).1/2.p.(l+l1+l2) --> à simplifier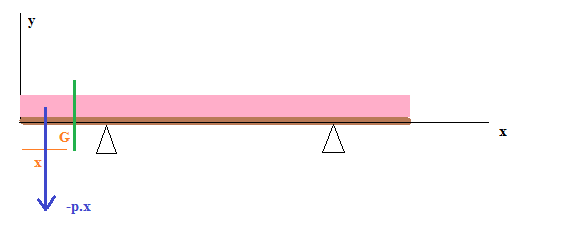



Ty = - (-p.x) = +p.x --> contrairement aux deux autres tronçon, on regarde ce qui est à gauche de G (plus simple), dans ce cas, la définition du torseur de cohésion nous dit qu'il faut mettre un signe "-"

Mfz = - (x/2.p.x) = -p.x²/2 --> effort x bas de levier.

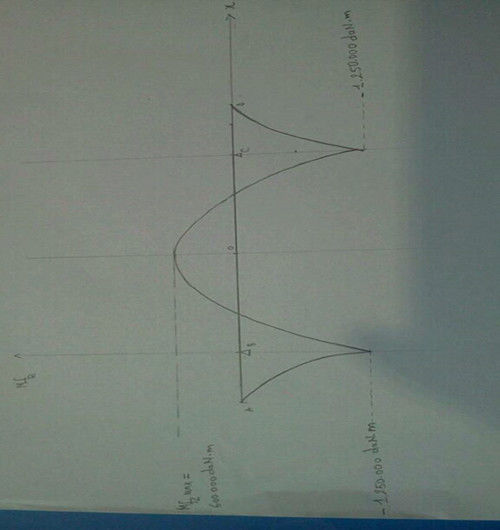
Tracé sur un cas simple
Juste pour m'assurer qu'on était ligné sur les diagrammes des effort tranchant et moment fléchissant, j'ai pris un cas simple :
l1 = L
l = 2L
l2 = l

J'obtiens bien les même allures que toi :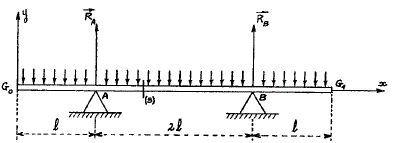





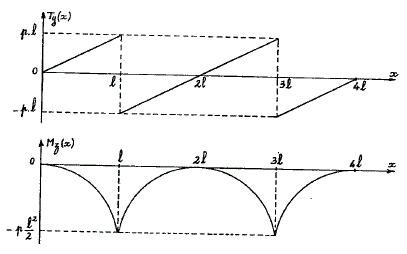
On constate bien la discontinuité de l'effort tranchant au niveau des appuis (qui introduisent une force verticale qu'on a calculée au tout début par un calcul statique).

En revanche le moment fléchissant est bien continus puisque qu'il n'y a pas de couples (flexions pures) introduits au niveau des appuis.

2. Relation à connaître pour vérifier la cohérence des tracés
Tu remarqueras désormais, si tu mets côte à côte les deux diagrammes que la relation

dMfz/dx = -Ty

dès que Ty est <0, Mfz croît, si Ty >0, Mfz décroît, et si Ty = 0, Mfz a atteint un extremum (maximum ou minimum) !

3. Conditions aux limites usuelles pour les appuis

Ces conditions aux limites se trouvent au niveau des appuis B et C :
* déplacement nul en ce point ;
* continuité du déplacement pour les tronçons à gauche et à droite de chaque appui.

Par exemple - pour déterminer des constantes d'intégration - on peut utiliser :
Si y(x) est le déplacement de la poutre pour une abscisse x, on utilise généralement pour un appui :
y(l1) = 0
y(l1+l) = 0

--> pas de déplacement au niveau de l'appui.

équation de continuité :
y'(l1+) = y'(l1-), idem pour l'autre appui.

4. Equation de la ligne élastique et flèche
Pour l'équation de la ligne élastique, peux-tu me donner les expressions que tu trouves pour les trois tronçons stp ?

Quelle est - d'après ton cours - la définition de la flèche ?

Bjr Gbm.juste un peu retard.
Etablir l equation de la ligne elastique sur le troncon BC.
Mfz=-p(l1+l2+l)² /2+p(l1+l2+l)/2
Soit L=(l1+l+l2) on a donc Mfz=-p² /2 +pl.x/2 + PL(l1+l-L)
Donc
E.I.y"=-px² /2 +pL.x/2+pL.(l1+l-L)
E.I.y'=-x³.p/6 +pL.x² /4 +pL.x(l1+l-)/2 + y'o
E.I.y=-x⁴.p/24 +x³ .PL/12 +x² pL.(l1+l-L) +y'o.x +yo

Conditions aux limites:
Y=0 si x=0 et y0=0
Y=0 si x=L/2   et y'0=x³ .p/6 -PL.x² /4 -PL.(l1+l-L).x/2
Pour x=L/2 a mi parcourt
Y'0=PL³ /48 - PL³ /16 -PL² .(l1+l-L)
Quand remplace cette expression dans y, on trouve
Y=-P.x.(x³ +2L.x² +L³ )/24.E.I
Equation de la ligne elastique.

La fleche au point o milieu de BC.
Au point o, x=L/2
Donc y =-5.PL/384.E.I
Et la fleche sur les troncons AB et CD on trouve y =- pl1⁴/8E.I et y=-pl2⁴ /8E.I
Car l equation de la ligne elastique est :
Y= -pl1³.x/6.E.I +p.x⁴ /24.E.I

Aussi sur mon diagramme des moments flechissants , le maximum est au dessus de o.x et non en dessous de 0 comme tu l as trace.donc essaies de voir .a tout a l heure.merci et bien de choses.

***Messages regroupés***

Alors, mes commentaires en bleu

Citation :
Etablir l equation de la ligne elastique sur le troncon BC.
Mfz=-p(l1+l2+l)² /2+p(l1+l2+l)/2
Soit L=(l1+l+l2) --> bonne pratique ! Cela te permet de faciliter ta double-intégration
on a donc Mfz=-p² /2 +pl.x/2 + PL(l1+l-L) --> Tu as simplifié, OK
Donc
E.I.y"=-px² /2 +pL.x/2+pL.(l1+l-L)
E.I.y'=-x³.p/6 +pL.x² /4 +pL.x(l1+l-)/2 + y'o
E.I.y=-x⁴.p/24 +x³ .PL/12 +x² pL.(l1+l-L) +y'o.x +yo

--> jusque-là, la méthode est correcte.

Conditions aux limites:
Y=0 si x=0 et y0=0 --> Aïe ! Je ne comprends pas pourquoi tu te place en x = 0, tu ne peux pas dire que Y = 0 car tu n'as pas d'appui, il est en x = l1 = L - l - l2 si je reprends tes notations. Comment justifies-tu cela ? Pourquoi ne pas prendre ma suggestion ?

Y=0 si x=L/2 --> ton déplacement ne peut pas être nul au milieu de ta poutre. C'est là que tu définis ta flèche = déplacement max. sur ce tronçon

et y'0=x³ .p/6 -PL.x² /4 -PL.(l1+l-L).x/2
Pour x=L/2 a mi parcourt
Y'0=PL³ /48 - PL³ /16 -PL² .(l1+l-L)
Quand remplace cette expression dans y, on trouve
Y=-P.x.(x³ +2L.x² +L³ )/24.E.I
Equation de la ligne elastique.

--> conditions aux limites à revoir et calculs à reprendre donc

La fleche au point o milieu de BC.
Au point o, x=L/2
Donc y =-5.PL/384.E.I --> à reprendre
Et la fleche sur les troncons AB et CD on trouve y =- pl1⁴/8E.I et y=-pl2⁴ /8E.I
--> tu n'expliques pas quelles conditions aux limites prises

Car l equation de la ligne elastique est :
Y= -pl1³.x/6.E.I +p.x⁴ /24.E.I

Aussi sur mon diagramme des moments flechissants , le maximum est au dessus de o.x et non en dessous de 0 comme tu l as trace.donc essaies de voir .a tout a l heure.merci et bien de choses.

--> attention, je n'ai pas dit que ton diagramme de moment fléchissant était faux, on aboutit à la même chose sauf que j'ai pris l1 = l2 = l/2 (noté L dans mon cas) pour SIMPLIFIER.

Bonjour Gbm.
Apres plusieurs jours je n arrive pas a trouver l equation de la ligne elastique avec les abscisses definies.ca rend encore plus difficiles la resolution.
Peux tu me proposer ta demarche?
Je pense que la mienne est claire.
Les conditions aux limites que j ai presente , sont fonction de l equation y que j ai trouve.
Dans cette equation , I'll y a deux constantes.pour trouver ces constantes dans cette eqyation , I'll. Faut donc poser des hypoteses pour trouver les valeurs de ces constantes.je n ai donc rien invente.
Donc essaies de voir.merci de repondre.cordialement.

Aussi Gbm,au milieu de la poutre console representee, la fleche maximum est egale a y = -pl⁴ /384.EI , et mes calculs le demontrent bien.
Ici L=l1+l+l2.
Donc reponds moi.merci

Aussi si je prend x=l+l1 sur le tronc BC comme tu l as indique , la fleche est egale a 0.ce qui n est pas normale du moment ou I'll y a un maximum sur ce troncon pour le moment flechissant.

La fleche est nulle aux appuis B et C.cela entraine yo=0.d autre part , la deformee est symetrique par rapport a l axe vertical passant par le milieu de BC.sa tangente est donc horizontale pour une abscisse x=L/2,d ou la valeur de la constante y'o.
Soit y'o(L/2)
Ensuite on remplace cette valeur dans l expression globale de y pour trouver l expression de l equation au milieu de .la travee.
Et on en deduit la fleche a cette abscisse qui est bien entendu le milieu de la travee BC.
Je pense que claire?

Salut,

Si tu estimes avoir appliqué la méthode tel qu'on en a discuté ensemble, c'est qu'on peut considérer que l'exercice est terminé.

C'est la méthode qui m'importe, pour les intégrations et calculs, je te fais confiance.

A+

Fais moi voir au moins ce que tu trouves dans ta methode.merci.