Inscription / Connexion Nouveau Sujet
Poussée d'Archimède
Bonjour, svp j'ai besoin d'aide.
On considère un cylindre circulaire, homogène de rayon R, de hauteur H, de masse volumique
, flottant sur un liquide de masse volumique
tel que l'axe du cylindre reste vertical.
1°)- Montrer que le liquide est plus dense que le cylindre.
2°)- Déterminer la position du métacentre M par rapport au centre de poussée C pour une
profondeur d'immersion h.
3°)- Trouver la relation existant entre les quantités H, R, et
pour que l'équilibre soit stable.
4°)- En déduire que si le rayon du cylindre est fixé, alors il existe une valeur Hmax que sa hauteur
ne doit pas dépasser pour qu'il flotte en équilibre stable sur tout liquide plus dense.
Mes résultats.
1) L'application directe du théorème d'Archimède repond à la question.
2) Je n'ai aucune idée
3) pour qu'il y ait premièrement équilibre, il faut que la force de poussée compense le poids du cylindre. Donc g.
2H=
g.
2h. Ainsi,
H=
h. Mais ça ne répond pas à la question.
4) aucune idée.
Bonjour
Le niveau des exercices montent brutalement ... 
As-tu étudié en cours la notion de métacentre ? (normalement oui si cet exercice t'est proposé)
Peux-tu illustrer cette notion par un schéma ?
Voici ce que dit mon support de cours :
Soit M le point d'intersection de la verticale du point A avec l'axe du
bateau qui passe par G lorsque tend vers 0 le point A tend vers la limite
; et le
point M tend vers un point limite que l'on appelle métacentre.
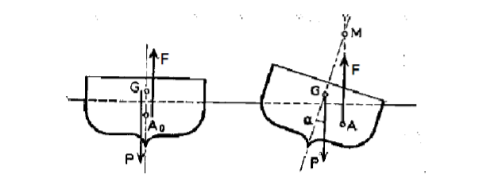
Où A0 et A représentent respectivement le centre de poussée à l'équilibre et à une position quelconque.
Bonjour Vanoise, dans mon cours une relation liant le centre de poussée au metacentre est donnée par : où I est le moment d'inertie de la surface de flottaison et V le volume immergé.
Le moment d'inertie en question est par rapport à quel axe?
Pour appliquer cette formule il me faut connaître le centre de poussée de la partie immergée. Soit C le centre de poussée. On a (ayant pris comme origine le point O centre de la surface de flottaison.) Les forces de pression s'exerçant sur la surface latérale du cylindre se compensent. Il reste uniquement les forces de pression s'exerçant sur la surface inférieure circulaire du cylindre. L'intégration du moment élémentaire de ces forces donne
. Si je suppose que C est sur l'axe du cylindre, le produit vectoriel sera nul. Soit C(r,
,z) on a finalement :
. Il n'y a aucune condition sur z et
. Donc tout point tel que
est un centre de poussée (c'est très bizarre car le centre de poussée est par définition le point d'application de la résultante des forces de pression, donc est unique).
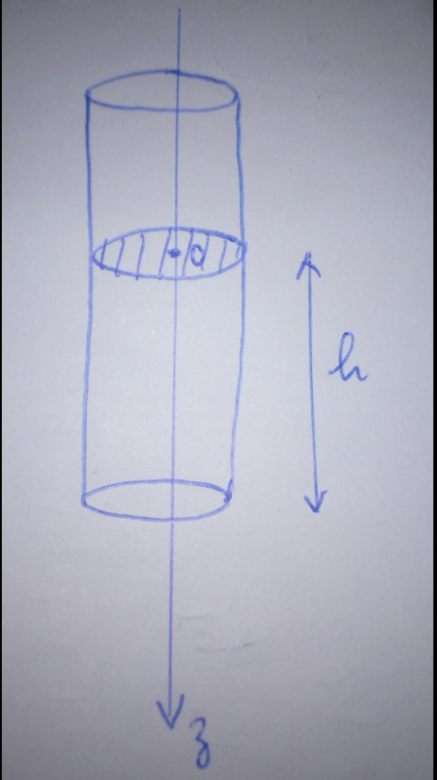
Dans le cas du cylindre en partie immergé d'axe vertical, la situation est très simple. La hauteur immergée s'obtient en considérant que le poids équilibre la poussée d'Archimède. Le centre de poussée est sur l'axe de symétrie, à mi hauteur de la partie immergée. Cette situation simple te permet de déterminer le volume V immergé qui reste le même lorsque le cylindre est incliné.
Reste à trouver la position de C lorsque le cylindre est incliné et cela ne me parait pas simple...


