en fait la poussée d'archimède est dirigée vers le haut tout comme la force de traction due au parachute et à l'air (qui tend à tout faire remonter).

L'association Pa+T s'oppose donc de plus en plus au poids de l'objet (donc à la pesanteur) au fur et à mesure que l'on injecte de l'air dans le parachute...

En fin de compte ce n'est pas Pa qui varie mais Pa+T puisque devient de plus en plus forte.

comment utilisé les valeurs numériques donné dans l'énoncé pour répondre aux questions ?

lulu3324, c'est un poil plus compliqué que cela.
  
L'énoncé, n'est pas très clair, qu'est ce qu'un parachute vient faire la dedans ?
  
Peut-être s'agit-il d'un ballon gonflable dans lequel on introduit de l'air (sorte de bouée).
  
Il faut alors savoir si les 18 litres d'air dont on parle est un volume à pression atmosphérique ou bien à la profondeur de 43 m. (l'énoncé devrait le préciser).
  
Et comme le volume d'air introduit (à une profondeur donnée), varie avec la pression (PV = nRT), donc aussi si la profondeur d'eau varie par la suite (en cours de remontée), la poussée d'Archimède sur le ballon varie aussi avec la profondeur instantanée.
...
Il est probable que la question 1 aurait du être
... en fonction de la profondeur et pas de la pesanteur.

Bref, un éclaircissement et/ou correction de l'énoncé serai(en)t le(s) bienvenu(s).

Bonjours J-P

Tu as raison j'ai commis une erreur en recopiant l'énoncé il s'agit bien du mot profondeur et non pas du mot pesanteur, mais pour le reste pas de changement il s'agit bien de l'énoncé de l'exercice que nous devons résoudre.

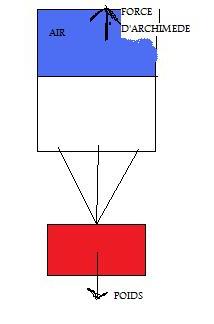
il y'a aussi un schéma ou l'on voit la brique reliée au'parachute' par des fils.
Le parachute dessiné est à moitié rempli d'air.

Essaie d'envoyer le dessin sur le site, cela deviendra probablement plus clair.

Voila le schémas que j'ai refais avec l'aide de paint.

adez moi svp , je doit le rendre pour demain

18 L d'air à 43 m de profondeur

Pression absolue à 43 m de profondeur = 101300 + 430000 = 531300 Pascal

PV = nRT
si T est constante, alors PV = constante = 531300 * 18.10^-3 = 9563 (SI)

Pression absolue (en Pascal) à profondeur x (en m) : P(x) = 101300 + 10000*x

P(x).V(x) = 9563

V(x) = 9563/(101300 + 10000*x)
Avec V(x) en m³ le volume occupé par l'air.

Donc la poussée d'archimède (en N) sur l'air est Pa1(x) = Rho_eau * g * V(x)  
Pa1(x) = 1000 * 9,81 * 9563/(101300 + 10000*x) = 9,38.10^7/(101300 + 10000*x)

La poussée d'Archimède sur l'objet est Pa2 = 1000 * 9,81 * 5.10^-3 = 49 N

La poussée d'Archimède totale est Pa(x) = 49 + 9,38.10^7/(101300 + 10000*x)

En négligeant le poids de l'air, l'objet se stabilisera à une profondeur X telle que Pa(X) = m.g

Soit: 49 + 9,38.10^7/(101300 + 10000*X) = 33 * 9,81

Soit X = 24 m
-----
Sauf distraction.