Inscription / Connexion Nouveau Sujet
potentiel quantique 1D
Bonjour,
Est ce que j'ai bien dessiné le potentiel de l'énoncé? J'ai un doute au niveau de la marche en a (j'ai mis v= + pour x=a ....
pour x=a ....
(voir photo ci-jointe)
Merci
***image supprimée***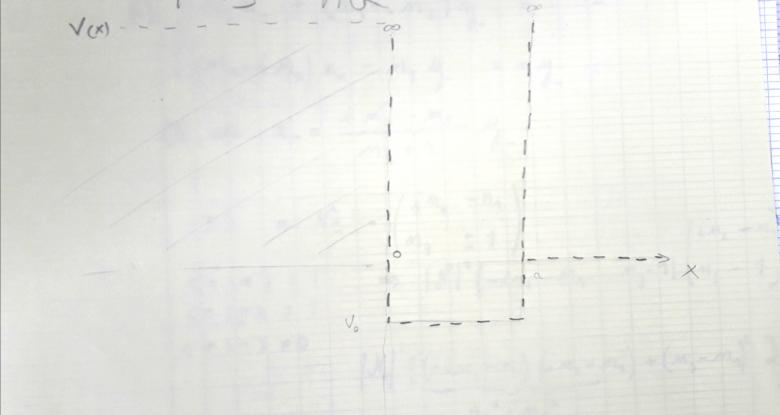
edit mmalou > ***image recadrée sur la figure***tu dois recopier ton énoncé si tu veux de l'aide bluq***
Bonjour
Entre x=(a- ) et x=(a+
) et x=(a+ ), il faut imaginer un pic de potentiel tel que laire sous la courbe représentant cette variation en fonction de x soit égale à v.
), il faut imaginer un pic de potentiel tel que laire sous la courbe représentant cette variation en fonction de x soit égale à v.
Puisque  tend vers zéro, la hauteur du pic tend vers l'infini comme tu l'as représenté. Attention tout de même : il ne s'agit pas d'une barrière de potentiel infranchissable comme en x=0.
tend vers zéro, la hauteur du pic tend vers l'infini comme tu l'as représenté. Attention tout de même : il ne s'agit pas d'une barrière de potentiel infranchissable comme en x=0.
Remarque : l'intégrale rappelée ci-dessus va être utile pour démontrer la relation de discontinuité en x=a de la dérivée par rapport à x de la fonction d'onde  '(x).
'(x).
Merci pour cette réponse.
Qu'est ce que v et pourquoi la fonction qui revrésente le potentiel est multiplié par v dans l'intégrale?
Ensuite on part d'une onde regressive qui arrive sur la barière de potentiel puis finalement une onde evanescante dans le quasi puit de potentiel?
A mon avis, il faut établir les expressions générales de  (x) comme solutions de l'équation de Schrödinger dans les deux domaines. Cela va te faire intervenir quatre constantes.
(x) comme solutions de l'équation de Schrödinger dans les deux domaines. Cela va te faire intervenir quatre constantes.
Il te faut donc quatre relations particulières :
1° :  (0) ?
(0) ?
2° : continuité de  (x) en x=a ?
(x) en x=a ?
3° : relation de discontinuité de la dérivée par rapport à x :  '(x) en x=a ?
'(x) en x=a ?
4° : limite de  (x) quand x
(x) quand x
 (onde évanescente comme tu l'as écrit).
(onde évanescente comme tu l'as écrit).
1) En x=0  =0 ?
=0 ?
3) la relation de discontinuité doit faire intervenir l'intégrale dont le delta de dirac est incompréhensible dans mon cours, auriez vous une réference sur le web?
1) En x=0
 =0 ?
=0 ?
3) la relation de discontinuité devant faire intervenir l'intégrale dont le delta de dirac est incompréhensible dans mon cours, auriez vous une réference sur le web?
On part de l'équation de Schrödinger :
On intègre par rapport à x entre et
:
On fait maintenant tendre vers zéro. On sait que
représente la densité de probabilité de présence de la particule. La fonction d'onde ne peut tendre vers l'infini. Nous avons donc :
Par définition de la fonction de Dirac :
A l'évidence :
Cela devrait te conduire à la relation de discontinuité sur la dérivée de la fonction d'onde. Sinon, compte tenu de la signification physique de la fonction d'onde rappelée au-dessus, la fonction d'onde est fonction continue de x en x= a. La continuité en x=0 conduit à . La suite est du calcul...



